Медиана в статистике: понятие, свойства и расчет

Примеры решения задач

Рассмотрим несколько простых задач на применение правила 3 сигм.

Задача 1

Имеется выборка жителей богатого дома. Средняя зарплата жильцов составляет 150 000 рублей, среднеквадратичное отклонение равно 20 000 рублей. Определите, жители с какой зарплатой вряд ли могут жить в этом доме: А) 205 000 рублей; Б) 95 000; В) 230 000; Г) 87 000.

Решение

Чтобы решить данную задачу, необходимо определить, каковы верхние и нижние границы возможных зарплат в доме. Для этого воспользуемся правилом 3 сигм.

\(s_{нижн.}=\mu-3\sigma=150\;000-3\cdot20\;000=150\;000-60\;000=90\;000\)

\(s_{верх.}=\mu+3\sigma=150\;000+3\cdot20\;000=150\;000+60\;000=210\;000\)

Значения А, Б входят в диапазон \(\left\). Значения В, Г не входят в него и, следовательно, являются искомыми грубыми ошибками.

Ответ: В, Г.

Задача 2

Завод выпускает партии по 100 цилиндрических деталей. Диаметр каждой детали — случайная величина, распределенная по нормальному закону. Математическое ожидание равно 65 мм, а среднее отклонение составляет 0,9 мм. Для упаковки партии используют коробки шириной 6600 мм. Детали кладут в один ряд. Если детали не поместятся в одну коробку, придется брать еще одну. Найдите вероятность, что понадобится только одна коробка.

Решение

Т. к. диаметр каждой детали распределен нормально, то и их общий диаметр также будет распределен нормально.

Чтобы все детали поместились в одну коробку, необходимо, чтобы отклонение диаметра всех деталей отклонялось от ожидаемого не более чем на 100 мм. Это следует из того, что математическое ожидание общего диаметра всех деталей равно \(65\cdot100=6500\). А ширина коробки составляет 6600 мм.

Для расчета воспользуемся формулами дисперсии и правилом 3 сигм, чтобы вычислить вероятность, что понадобится только одна коробка.

\(P\left|X-M(X)\right|<100\;\Rightarrow2\Phi\left=2\Phi\left=2\cdot0,3665=0,733\)

Доказательство времени работы O ( n )

Рекурсивный вызов с вычислением медианы не превышает линейное поведение в худшем случае, потому что список медиан имеет размер , в то время как другой рекурсивный вызов рекурсивно повторяется не более чем на 70% списка. Пусть будет время, необходимое для запуска алгоритма медианы медианы Quickselect для массива размера . Тогда мы знаем, что это время:
п5{\ displaystyle {\ frac {n} {5}}}Т(п){\ Displaystyle Т (п)}п{\ displaystyle n}

Т(п)≤Т(п5)+Т(п⋅710)+c⋅п.{\ Displaystyle Т (п) \ Leq Т (п / 5) + Т (п \ CDOT 7/10) + с \ CDOT п.}

куда

• часть для нахождения истинной медианы медиан, путем запуска (независимый) Быстрого выбор на них (так как найти медиану только частный случай выбора K -smallest элемента)Т(п5){\ Displaystyle Т ({\ гидроразрыва {п} {5}})}п5{\ displaystyle {\ frac {n} {5}}}
• термин является для разделения работы , чтобы создать две стороны, одна из которых наши будет RECURSE Быстрого выбора (мы посетили каждый элемент постоянного число раз, чтобы сформировать их в п / 5 групп и принимать каждую медиану в время).О(п){\ Displaystyle О (п)}c⋅п{\ displaystyle c \ cdot n}О(1){\ displaystyle O (1)}
• часть для фактического рекурсии (Быстрый выбор для наихудшего случая, в котором K -й элемент находится в большом разделе, могут быть размером максимально)Т(7п10){\ Displaystyle Т ({\ гидроразрыва {7n} {10}})}7п10{\ displaystyle {\ frac {7n} {10}}}

Отсюда с помощью индукции легко показать, что

Т(п)≤10⋅c⋅п∈О(п).{\ Displaystyle Т (п) \ Leq 10 \ CDOT с \ CDOT п \ в О (п).}

Алгоритм

Как указывалось ранее, медиана медианы используется в качестве стратегии опорного выбора в алгоритме быстрого выбора , который в псевдокоде выглядит следующим образом. Будьте осторожны в обращении , и при реализации. В следующем псевдокоде предполагается, что , и в списке используется нумерация с единицей, которая изначально вызывается с 1 в качестве аргумента и длиной списка в качестве аргумента

Обратите внимание, что это возвращает индекс n-го наименьшего числа после перестановки списка, а не фактическое значение n-го наименьшего числа.

function select(list, left, right, n)
    loop
        if left = right then
            return left
        pivotIndex := pivot(list, left, right)
        pivotIndex := partition(list, left, right, pivotIndex, n)
        if n = pivotIndex then
            return n
        else if n < pivotIndex then
            right := pivotIndex - 1
        else
            left := pivotIndex + 1

Существует подпрограмма, называемая разделением, которая может за линейное время сгруппировать список (от индексов до ) на три части: те, которые меньше определенного элемента, те, которые равны ему, и те, которые больше, чем элемент ( трехстороннее разделение ). Группировка на три части гарантирует, что медиана медианы поддерживает линейное время выполнения в случае многих или всех совпадающих элементов. Вот псевдокод, который выполняет раздел об элементе :

function partition(list, left, right, pivotIndex, n)
    pivotValue := list
    swap list and list  // Move pivot to end
    storeIndex := left
    // Move all elements smaller than the pivot to the left of the pivot
    for i from left to right − 1 do
        if list < pivotValue then
            swap list and list
            increment storeIndex
    // Move all elements equal to the pivot right after
    // the smaller elements
    storeIndexEq = storeIndex
    for i from storeIndex to right − 1 do
        if list = pivotValue then
            swap list and list
            increment storeIndexEq
    swap list and list  // Move pivot to its final place
    // Return location of pivot considering the desired location n
    if n < storeIndex then
        return storeIndex  // n is in the group of smaller elements
    if n ≤ storeIndexEq then
        return n  // n is in the group equal to pivot
    return storeIndexEq // n is in the group of larger elements

Подпрограмма pivot — это фактический алгоритм медианы из медиан. Он делит свой ввод (список длины n ) на группы, состоящие не более чем из пяти элементов, вычисляет медиану каждой из этих групп с помощью некоторой подпрограммы, а затем рекурсивно вычисляет истинную медиану медиан, найденных на предыдущем шаге :

Обратите внимание, что сводные вызовы select ; это пример взаимной рекурсии .
п5{\ displaystyle {\ frac {n} {5}}}

function pivot(list, left, right)
    // for 5 or less elements just get median
    if right − left < 5 then
        return partition5(list, left, right)
    // otherwise move the medians of five-element subgroups to the first n/5 positions
    for i from left to right in steps of 5
        // get the median position of the i'th five-element subgroup
        subRight := i + 4
        if subRight > right then
            subRight := right
        median5 := partition5(list, i, subRight)
        swap list and list[left + floor((i − left)/5)]

    // compute the median of the n/5 medians-of-five
    mid := (right − left) / 10 + left + 1
    return select(list, left, left + floor((right − left) / 5), mid)

Partition5 подпрограмма выбирает медиану группы не более пяти элементов; простой способ реализовать это — сортировка вставкой , как показано ниже. Его также можно реализовать в виде дерева решений .

function partition5( list, left, right)
    i := left + 1
    while i ≤ right
        j := i
        while j > left and list > list do
            swap list and list
            j := j − 1
        i :=  i + 1
            
    return floor((left + right) / 2)

Неуникальность значения

Если имеется чётное количество случаев и два средних значения различаются, то медианой, по определению, может служить любое число между ними (например, в выборке {1, 3, 5, 7} медианой может служить любое число из интервала (3,5)). На практике в этом случае чаще всего используют среднее арифметическое двух средних значений (в примере выше это число (3+5)/2=4). Для выборок с чётным числом элементов можно также ввести понятие «нижней медианы» (элемент с номером n/2 в упорядоченном ряду из элементов; в примере выше это число 3) и «верхней медианы» (элемент с номером (n+2)/2; в примере выше это число 5). Эти понятия определены не только для числовых данных, но и для любой порядковой шкалы.

Размах выборки

Следующий важная характеристика ряда данных – это размах выборки.

Если выборка представлена в виде упорядоченного ряда данных, то достаточно вычесть из последнего числа ряда первое число. Так, размах выборки результатов теста в классе равен:

25 – 12 = 13,

так как самые лучшие ученики смогли решить все 25 заданий, а наихудший учащийся ответил правильно только на 13 вопросов.

Размах выборки характеризует стабильность, однородность исследуемых свойств. Например, пусть два спортсмена-стрелка в ходе соревнований производят по 5 выстрелов по круговой мишени, где за попадание начисляют от 0 до 10 очков. Первый стрелок показал результаты 8, 9, 9, 8, 9 очков. Второй же спортсмен в своих попытках показал результаты 7, 10, 10, 6, 10. Средние арифметические этих рядов равны:

(8+9+9+8+9):5 = 43:5 = 8,6;

(7+10+10+6+10):5 = 43:5 = 8,6.

Получается, что в среднем оба стрелка стреляют одинаково точно, однако первый спортсмен демонстрирует более стабильные результаты. У его выборки размах равен

9 – 8 = 1,

в то время как размах выборки второго спортсмена равен

10 – 6 = 4.

Размах выборки может быть очень важен в метеорологии. Например, в Алма-Ате и Амстердаме средняя температура в течение года почти одинакова и составляет 10°С. Однако в Алма-Ате в январе и феврале иногда фиксируются температуры ниже -30°С, в то время как в Амстердаме за всю историю наблюдений она никогда не падала ниже -20°С.

Примеры решения задач

Нет ничего приятнее, чем поупражняться и поискать градусы и длины в равнобедренном треугольнике. Ну… почти ничего.

Задачка раз. Дан ABC: ∠C = 80∘, AB = BC. Найдите ∠B.

Поскольку вы уже знакомы с пятью теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны.
∠A = ∠C = 80∘.
Не должно вас удивить и то, что сумма углов треугольника равна 180∘
∠B = 180∘ − 80∘ − 80∘ = 20∘.
∠B = 20∘

Задачка два. В равнобедренном треугольнике один из углов равен 110∘. Найдите наибольший из внешних углов этого треугольника.

Вспоминаем первую теорему о равенстве углов при основании (а лучше не забываем вовсе). Поскольку сумма углов = 180∘, то второго угла в 110∘ в нём быть не может. Соответственно, известный угол в 110∘ — это угол при вершине. (180∘−110∘)/2=35∘. Внешние углы треугольника равны: 180∘−110∘=70∘,180∘−35∘=145∘,180∘−35∘=145∘. Больший внешний угол равен 145∘

Расчет медианы в Excel

Медиану для числовых данных легко найти, используя функцию Excel, которая так и называется — МЕДИАНА. Другое дело интервальные данные. Соответствующей функции в Excel нет. Поэтому нужно задействовать приведенную выше формулу. Что поделаешь? Но это не очень трагично, так как расчет медианы по интервальным данным – редкий случай. Можно и на калькуляторе разок посчитать.

Напоследок предлагаю задачку. Имеется набор данных. 15, 5, 20, 5, 10. Каково среднее значение? Четыре варианта:

а) 11;

б) 5;

в) 10;

г) 5, 10, 11.

Мода, медиана и среднее значение выборки – это разный способ определить центральную тенденцию в выборке.

Ниже видеоролик о том, как рассчитать медиану в Excel.

https://youtube.com/watch?v=ZDHH8hogq0A

Среднее арифметическое выборки

Сбор информации о выборке является лишь первой стадией статистического исследования. Далее ее необходимо обобщить, то есть получить некоторые цифры, характеризующие выборку. Самой часто используемой статистической характеристикой является среднее арифметическое.

Другими словами, для подсчета среднего арифметического необходимо просто сложить все числа в ряде данных, а потом поделить получившееся значение на количество чисел в ряде. Так, в примере с тестом по математике (таблица 1) средний балл учащихся составит: (12+19+19+14+17+16+18+20+15+25+13+20+25+16+17+12+24+13+21+13):20=

= 349:20 = 17,45.

Среднее арифметическое позволяет одним числом характеризовать какое-либо качество всех объектов группы. Чем больше средний балл учащихся в классе, тем выше их успеваемость. Чем меньше среднее количество голов, пропускаемых футбольной командой за один матч, тем лучше она играет в обороне. Если средняя зарплата программистов в городе составляет 90 тысяч рублей, а дворников – 25 тысяч рублей, то это значит, что программисты значительно более востребованы на рынке труда, а потому при выборе будущей профессии лучше предпочесть именно эту специальность.

Свойства

Медиана, независимо от типа треугольника, имеет 5 характерных черт:

1. Если нарисовать из каждой вершины по одной прямой, то можно найти центр тяжести. Именно место пересечения всех 3 лучей и будет точкой равновесия.
2. Также, переплетаясь, они рассекают объект на 6 одинаковых по площади сегментов.
3. Исходя из этого, можно сделать вывод, что 1 луч рассекает треугольник на 2 куска с равной площадью. В случае равнобедренных треугольников и с равными сторонами получившиеся сегменты даже являются симметричными.
4. Самой большей стороне соответствует самая маленькая прямая. В случае равносторонней фигуры, соответственно, все 3 будут иметь одну и ту же длину.
5. Соединяясь, лучи делят друг друга в соотношении 1 к 2.

Анализ

Ключевым шагом является сокращение проблемы до выбора в двух списках, общая длина которых меньше, чем исходный список, плюс линейный коэффициент для шага сокращения. Это позволяет простой индукцией показать, что общее время работы линейно.

Конкретный выбор групп из пяти элементов объясняется следующим образом. Во-первых, вычисление медианы нечетного списка происходит быстрее и проще; хотя можно использовать четный список, для этого требуется взять среднее значение двух средних элементов, что медленнее, чем простой выбор одного точного среднего элемента. Во-вторых, пять — это наименьшее нечетное число, при котором работает медиана медиан. С группами только из трех элементов результирующий список медиан для поиска имеет длину и сокращает список до рекурсивной длины , поскольку он больше 1/2 × 2/3 = 1/3 элементов и меньше 1 / 2 × 2/3 = 1/3 элементов. Таким образом, это по-прежнему оставляет элементы для поиска, не уменьшая проблему в достаточной степени. Однако отдельные списки короче, и можно ограничить результирующую сложность методом Акра – Бацци , но это не доказывает линейность.
п3{\ displaystyle {\ frac {n} {3}}}23п{\ displaystyle {\ frac {2} {3}} п}п{\ displaystyle n}О(пбревно⁡п){\ Displaystyle О (п \ журнал п)}

И наоборот, вместо этого можно сгруппировать по семи, девяти или более элементам, и это действительно работает. Это уменьшает размер списка медиан до , и размера списка , чтобы рекурсия в асимптоты в 3 н / 4 (75%), так как квадранты в приведенном выше таблице приблизительно 25%, а размере перекрывающихся линий уменьшается пропорционально. Это уменьшает коэффициент масштабирования с 10 асимптотически до 4, но, соответственно, увеличивает срок работы по разделению. Поиск медианы для более крупной группы занимает больше времени, но является постоянным фактором (зависит только от ) и, таким образом, не меняет общую производительность по мере роста n . Фактически, учитывая количество сравнений в худшем случае, постоянный коэффициент равен .
грамм{\ displaystyle g}пграмм{\ displaystyle {\ frac {n} {g}}}c{\ displaystyle c}грамм{\ displaystyle g}2грамм(грамм-1)грамм-3{\ displaystyle {\ frac {2g (g-1)} {g-3}}}

Если вместо этого сгруппировать другой способ, скажем, разделив список элементов на 5 списков, вычислив медиану каждого, а затем вычислив медиану из них, т. Е. Группируя по постоянной доле, а не по постоянному числу, то сокращение не будет столь очевидным. проблема, поскольку для этого требуется вычисление 5 медиан, каждое в списке элементов, а затем рекурсивное обращение к списку максимальной длины . Как и в случае группировки по 3, отдельные списки короче, но общая длина не меньше — фактически больше — и, таким образом, можно доказать только сверхлинейные границы. Группировка списков длины в квадрат также сложна.
п{\ displaystyle n}п5{\ displaystyle {\ frac {n} {5}}}710п{\ displaystyle {\ frac {7} {10n}}}п{\ displaystyle {\ sqrt {n}}}п{\ displaystyle {\ sqrt {n}}}

Формулы равнобедренного треугольника

Формулы сторон равнобедренного треугольника

b — основание равнобедренного треугольника

a — равные стороны равнобедренного треугольника

α — углы при основании

β — угол, образованный равными сторонами

Формулы длины стороны (основания b) равнобедренного треугольника

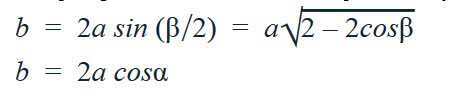
Формулы длины равных сторон равнобедренного треугольника (стороны a):

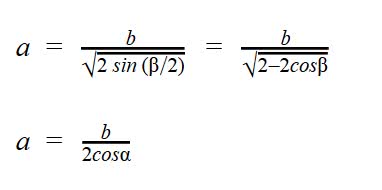
Формулы высоты, медианы, биссектрисы равнобедренного треугольника

b — основание равнобедренного треугольника

a — равные стороны равнобедренного треугольника

α — углы при основании

β — угол, образованный равными сторонами

L — высота, биссектриса и медиана

Формулы высоты, биссектрисы и медианы равнобедренного треугольника, через сторону и угол (L)

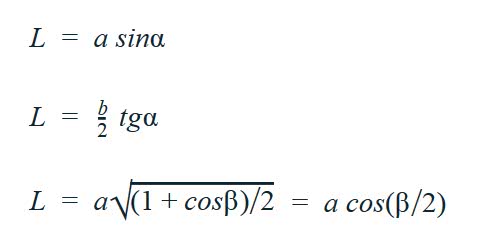
Формула высоты, биссектрисы и медианы равнобедренного треугольника, через стороны (L)

Определение моды и медианы графическим методом

Моду и медиану в интервальном ряду можно определить графически. Мода определяется по гистограмме распределения. Для этого выбирается самый высокий прямоугольник, который является в данном случае модальным. Затем правую вершину модального прямоугольника соединяем с правым верхним углом предыдущего прямоугольника. А левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Из точки их пересечения опускаем перпендикуляр на ось абсцисс. Абсцисса точки пересечения этих прямых и будет модой распределения (рис. 3). Рис. 3. Графическое определение моды по гистограмме. Рис. 3. Графическое определение моды по гистограмме. Рис. 4. Графическое определение медианы по кумуляте Для определения медианы из точки на шкале накопленных частот (частостей), соответствующей 50 %, проводится прямая, параллельная оси абсцисс до пересечения с кумулятой. Затем из точки пересечения опускается перпендикуляр на ось абсцисс. Абсцисса точки пересечения является медианой.

Теория для решения данных задач. Формулы для расчета моды и медианы

Модой в статистике называется величины признака (варианта), которая чаще всего встречается в данной совокупности.

Медианой в статистике называется варианта, которая находится в середине вариационного ряда. Медиана делит ряд пополам. Обозначают медиану символом.

Распределительные средние – мода и медиана, их сущность и способы исчисления.

Данные показатели относятся к группе распределительных средних и используются для формирования обобщающей характеристики величины варьирующего признака.

Мода – это наиболее часто встречающееся значение варьирующего признака в вариационном ряду. Модой распределения называется такая величина изучаемого признака, которая в данной совокупности встречается наиболее часто, т.е. один из вариантов признака повторяется чаще, чем все другие. Для дискретного ряда (ряд, в котором значение варьирующего признака представлены отдельными числовыми показателями) модой является значение варьирующего признака обладающего наибольшей частотой. Для интервального ряда сначала определяется модальный интервал (т.е. содержащий моду), в случае интервального распределения с равными интервалами определяется по наибольшей частоте; с неравными интервалами – по наибольшей плотности, а определение моды требует проведения расчетов на основе следующих формул:

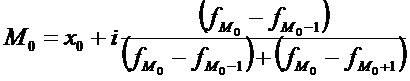
где:- нижняя граница модального интервала;

— величина модального интервала;

— частота модального интервала;

— частота интервала, предшествующего модальному;

— частота интервала, следующего за модальным;

Для определения медианы в дискретном ряду при наличии частот, сначала исчисляется полусумма частот, а затем определяется какое значение варьирующего признака ей соответствует. При исчислении медианы интервального ряда сначала определяются медианы интервалов, а затем определяется какое значение варьирующего признака соответствует данной частоте. Для определения величины медианы используется формула:

где:- нижняя граница медианного интервала;

— величина медианного интервала;

— накопленная частота интервала, предшествующего медианному;

— частота медианного интервала;

Медианный интервал не обязательно совпадает с модальным.

Формула медианы

Формула медианы в статистике для дискретных данных чем-то напоминает формулу моды. А именно тем, что формулы как таковой нет. Медианное значение выбирают из имеющихся данных и только, если это невозможно, проводят несложный расчет.

Первым делом данные ранжируют (сортируют по убыванию). Далее есть два варианта. Если количество значений нечетно, то медиана будет соответствовать центральному значению ряда, номер которого можно определить по формуле:

где

№_Me – номер значения, соответствующего медиане,

N – количество значений в совокупности данных.

Тогда медиана обозначается, как

Это первый вариант, когда в данных есть одно центральное значение. Второй вариант наступает тогда, когда количество данных четно, то есть вместо одного есть два центральных значения. Выход прост: берется средняя арифметическая из двух центральных значений:

В интервальных данных выбрать конкретное значение не представляется возможным. Медиану рассчитывают по определенному правилу. 

Для начала (после ранжирования данных) находят медианный интервал. Это такой интервал, через который проходит искомое медианное значение. Определяется с помощью накопленной доли ранжированных интервалов. Где накопленная доля впервые перевалила через 50% всех значений, там и медианный интервал.

Не знаю, кто придумал формулу медианы, но исходили явно из того предположения, что распределение данных внутри медианного интервала равномерное (т.е. 30% ширины интервала – это 30% значений, 80% ширины – 80% значений и т.д.). Отсюда, зная количество значений от начала медианного интервала до 50% всех значений совокупности (разница между половиной количества всех значений и накопленной частотой предмедианного интервала), можно найти, какую долю они занимают во всем медианном интервале. Вот эта доля аккурат переносится на ширину медианного интервала, указывая на конкретное значение, именуемое впоследствии медианой.

Обратимся к наглядной схеме.

Немного громоздко получилось, но теперь, надеюсь, все наглядно и понятно. Чтобы при расчете каждый раз не рисовать такой график, можно воспользоваться готовой формулой. Формула медианы имеет следующий вид:

где x_Me — нижняя граница медианного интервала;

i_Me — ширина медианного интервала;

∑f/2 — количество всех значений, деленное на 2 (два);

S_(Me-1)— суммарное количество наблюдений, которое было накоплено до начала медианного интервала, т.е. накопленная частота предмедианного интервала;

f_Me — число наблюдений в медианном интервале.

Как нетрудно заметить, формула медианы состоит из двух слагаемых: 1 – значение начала медианного интервала и 2 – та самая часть, которая пропорциональна недостающей накопленной доли до 50%. 

Для примера рассчитаем медиану по следующим данным.

Требуется найти медианную цену, то есть ту цену, дешевле и дороже которой по половине количества товаров. Для начала произведем вспомогательные расчеты накопленной частоты, накопленной доли, общего количества товаров.

По последней колонке «Накопленная доля» определяем медианный интервал – 300-400 руб (накопленная доля впервые более 50%). Ширина интервала – 100 руб. Теперь остается подставить данные в приведенную выше формулу и рассчитать медиану.

То есть у одной половины товаров цена ниже, чем 350 руб., у другой половины – выше. Все просто. Средняя арифметическая, рассчитанная по этим же данным, равна 355 руб. Отличие не значительное, но оно есть.

Использование функции MEDIAN в Microsoft Excel

В Excel есть несколько функций, которые рассчитывают часто используемые средние значения. Функция MEDIAN находит медиану или среднее значение в списке чисел.

Примечание . Эти инструкции относятся к Excel 2019, 2016, 2013, 2010, Excel 2019 для Mac, Excel 2016 для Mac, Excel для Mac 2011, Excel для Office 365 и Excel Online.

Как работает функция MEDIAN

Функция MEDIAN сортирует предоставленные аргументы, чтобы найти значение, которое арифметически падает в середине группы.

Если существует нечетное количество аргументов, функция идентифицирует среднее значение в диапазоне как среднее значение.

Если имеется четное число аргументов, функция принимает среднее арифметическое или среднее из двух средних значений.

аргументы

Значения, предоставляемые в качестве аргументов, не обязательно должны быть в каком-то определенном порядке для работы функции. Вы можете увидеть это в игре в четвертом ряду на примере изображения ниже.

MEDIAN Синтаксис функции

Синтаксис функции относится к макету функции и включает имя функции, скобки, разделители запятых и аргументы.

Ниже приведен синтаксис для функции MEDIAN:

  = MEDIAN (  Number1  ,   Number2  ,   Number3  ,  ... )  

• = MEDIAN . Все формулы MEDIAN начинаются таким образом.
• Number1 Обязательные данные, которые должны быть рассчитаны функцией.
• Number2 Необязательные дополнительные значения данных для расчета в среднем. Максимально допустимое количество записей – 255, каждая из которых должна быть разделена запятой.

Этот аргумент может содержать:

• Список чисел для усреднения
• Ячейки ссылаются на расположение данных на листе
• Диапазон ссылок на ячейки
• Именованный диапазон

Варианты ввода функции и ее аргументов:

• Ввод полной функции, например = MEDIAN (A2: F2) , в ячейку листа
• Ввод функции и аргументов с использованием диалогового окна функции

Пример функции MEDIAN

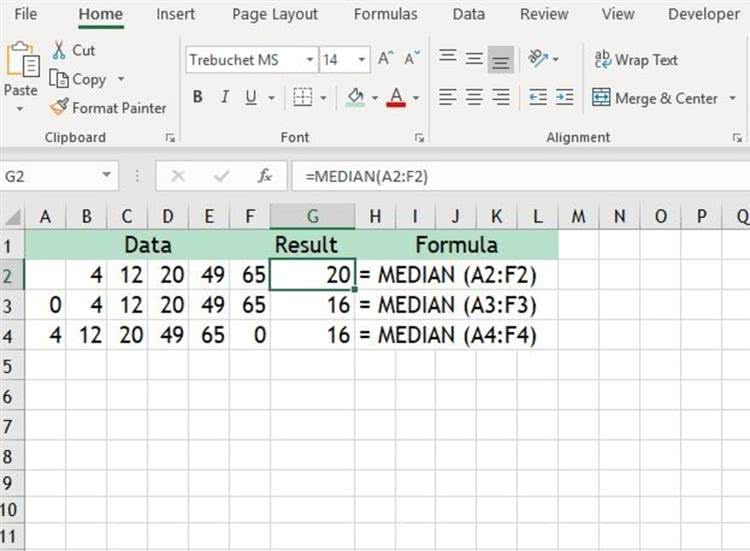
Эти шаги подробно описывают, как ввести функцию MEDIAN и аргументы, используя диалоговое окно для первого примера, показанного на изображении выше.

1. Нажмите на ячейку G2 , где будут отображаться результаты.
2. Нажмите кнопку Вставить функцию , чтобы открыть диалоговое окно «Вставить функцию».
3. Выберите Статистический в списке категорий.
4. Выберите MEDIAN в списке функций и нажмите ОК .
5. Выделите ячейки от A2 до F2 на листе, чтобы автоматически вставить этот диапазон.
6. Нажмите Enter , чтобы завершить функцию и вернуться к рабочему листу.

Ответ 20 должен появиться в ячейке G2

Если щелкнуть ячейку G2, полная функция = MEDIAN (A2: F2) появится в строке формул над рабочим листом.

Почему медиана 20? Для первого примера в изображении, поскольку существует нечетное количество аргументов (пять), среднее значение вычисляется путем нахождения среднего числа. Здесь 20, потому что есть два числа больше (49 и 65) и два числа меньше (4 и 12).

Пустые ячейки против нулевых значений

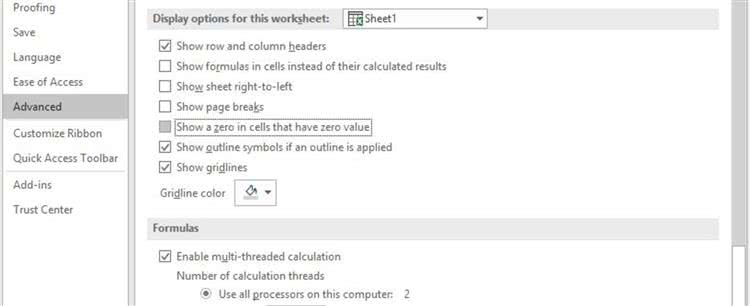
При нахождении медианы в Excel, есть разница между пустыми или пустыми ячейками и теми, которые содержат нулевое значение.

Как показано в приведенных выше примерах, функция MEDIAN игнорирует пустые ячейки, но не ячейки, содержащие нулевое значение.

• Медиана изменяется между первым и вторым примерами, потому что в ячейку A3 был добавлен ноль, а ячейка A2 пуста.
• Добавление ноля к ячейке A3 изменяет число аргументов, передаваемых функции в ячейке G3, с пяти до шести – четное число. В результате медиана рассчитывается путем сложения двух средних значений (12 и 20) вместе, а затем деления на два, чтобы найти их среднее значение (16).

По умолчанию Excel отображает ноль (0) в ячейках с нулевым значением, как показано в примере выше. Эту опцию можно отключить, и, если это будет сделано, такие ячейки останутся пустыми, но нулевое значение для этой ячейки все еще будет включено в качестве аргумента функции при вычислении медианы.

Примечание . Этот параметр нельзя отключить в Excel Online.

Как включить или отключить этот параметр в Excel 2019, Excel 2016, Excel 2013 и Excel 2010 :

1. Перейдите на вкладку Файл и нажмите Параметры .
2. Перейдите в категорию Дополнительно на левой панели параметров.
3. На правой стороне прокручивайте вниз, пока не найдете раздел Параметры отображения для этого рабочего листа .
4. Чтобы скрыть нулевые значения в ячейках, снимите флажок Показать ноль в ячейках с нулевым значением . Чтобы отобразить нули, поставьте галочку в поле.
5. Сохраните любые изменения с помощью кнопки ОК .

Как включить или отключить этот параметр в Excel 2019 для Mac, Excel 2016 для Mac и Excel для Mac 2011 :

1. Перейдите в меню Excel .
2. Нажмите Настройки .
3. Нажмите Вид в разделе «Авторизация».
4. Снимите флажок Показать нулевые значения в разделе Параметры окна .

Что такое Медиана?

Медиана – это среднее число в отсортированном, возрастающем или убывающем, списке чисел, и оно может быть более информативным для этого набора данных, чем среднее.

Ключевые моменты

• Медиана – это среднее число в отсортированном, возрастающем или убывающем, списке чисел, и оно может быть более информативным для этого набора данных, чем среднее.
• Медиана иногда используется вместо среднего, когда в последовательности есть выбросы, которые могут исказить среднее значение.
• Если имеется нечетное количество чисел, среднее значение – это число, которое находится в середине, с одинаковым количеством чисел внизу и вверху.
• Если в списке есть четное количество чисел, необходимо определить среднюю пару, сложить вместе и разделить на два, чтобы найти среднее значение.

МЕДИАНА ТРЕУГОЛЬНИКА

Слово «медиана» переводится как «равноделящая сторону». Чтобы построить медиану, надо середину стороны треугольника соединить отрезком с противолежащей вершиной треугольника. Полученный отрезок и есть медиана треугольника.

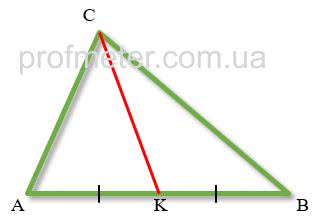
Медиана треугольника – отрезок, проведенный из вершины треугольника, соединяющий эту вершину с серединой противолежащей стороны треугольника.

На рисунке красным цветом обозначена медиана CK. При этом она делит сторону AB треугольника пополам, AK = KB.

Свойства медианы треугольника

Все медианы треугольника пересекаются в одной точке, расположенной в плоскости треугольника и являющейся его центром тяжести. 

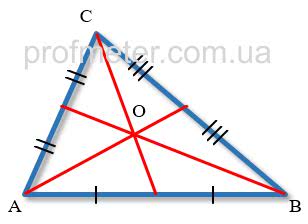
Для определения этой точки достаточно построить две медианы треугольника, и точка их пересечения будет принадлежать третьей медиане этого треугольника.

• Точкой пересечения медиан треугольника каждая медиана делится в отношении 2:1, считая от вершины треугольника. Т.е. длина отрезка медианы от вершины треугольника до точки пересечения медиан составляет 2/3 всей ее длины, а от точки пересечения медиан до стороны треугольника — 1/3 ее длины.

• Медиана разбивает треугольник на два равновеликих (по площади) треугольника.

• Треугольник делится тремя медианами на шесть равновеликих треугольников.

• Из отрезков, образующих медианы, можно составить треугольник, площадь которого будет равна 3/4 от всего треугольника. Длины медиан удовлетворяют неравенству треугольника.

• В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.

• Большей стороне треугольника соответствует меньшая медиана.

• У равнобедренного треугольника медиана, биссектриса и высота, проведенные к основанию треугольника, совпадают.

• У равностороннего треугольника все три «замечательные» линии (высота, биссектриса и медиана) совпадают и три «замечательных» точки (точки ортоцентра, центра тяжести и центра вписанной и описанной окружностей) находятся в одной точке пересечения «замечательных» линий, т.е. тоже совпадают.

Формулы медианы произвольного треугольника

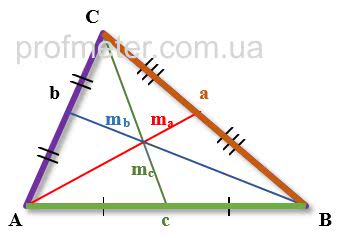
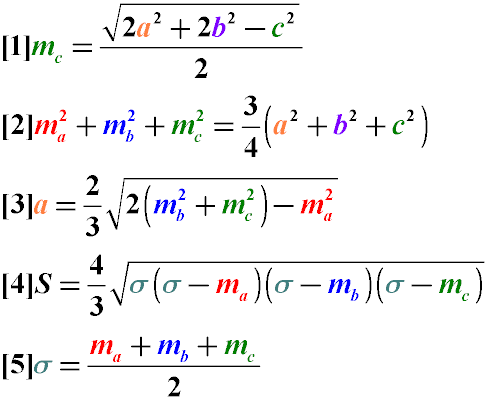
• Длина медианы, проведенной к стороне произвольного треугольника равна половине квадратного корня из удвоенной суммы квадратов двух других сторон из которой вычтен квадрат стороны, к которой проведена медиана (Формула 1)
• Сумма квадратов медиан треугольника равна 3/4 суммы квадратов его сторон (Формула 2)
• Длина стороны треугольника равна 2/3 квадратного корня из удвоенной суммы квадратов медиан, проведенных к двум другим его сторонам за вычетом квадрата медианы, проведенной к искомой стороне (Формула 3)
• Площадь треугольника можно найти через длины его медиан, используя значение полусуммы длин медиан (Формулы 4 и 5)

Содержание главы:

Как найти длину медианы треугольника

Нахождение площади через медианы

Угол между высотой и медианой треугольника

Медиана прямоугольного треугольника

Медіана прямокутного трикутника

Площадь треугольникаОписание курса Как найти длину медианы треугольника   

Похожие записи:

Как пользоваться посудомоечной машиной bosch: правила и нюансы эксплуатации Зеленый лук Чернослив вяленый. как сушить сливу в домашних условиях Лучшие полироли для мебели Узнайте, какие варенья приносят наибольшую пользу. самые полезные виды варенья Храни в холодильнике, не передерживай. что нужно знать о патчах