Содержание
Первый признак равенства треугольников
Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.
Давайте рассмотрим три признака равенства треугольников.
Теорема 1. Равенство треугольников по двум сторонам и углу между ними.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Даны два треугольника △ABC и △A1B1C1, у которых AC = A1C1, AB = A1B1, ∠A = ∠A1.
Докажите, что △ABC = △A1B1C1.
Доказательство:
При наложении △A1B1C1 на △ABC вершина A1 совмещается с вершиной A, и сторона A1B1 накладывается на сторону AB, AC — на сторону A1C1.
Сторона A1B1 совмещается со стороной AB, вершина B совпадает с вершиной B1, сторона A1С1 совмещается со стороной AС, вершина C совпадает с вершиной C1.
Значит, происходит совмещение вершин В и В1, С и С1.
B1C1 = BC, следовательно, △ABC совмещается с △A1B1C, значит, △ABC = △A1B1C1.
Теорема доказана.
Важно!
Первый признак используют при доказательстве второго и третьего признаков равенства треугольников.
Познавайте математику вместе с нашими лучшими преподавателями на занятиях по математике для учеников с 1 до 11 класса!
Как найти катет равнобедренного треугольника если известна гипотенуза | Помощь школьнику
урок: Повторение темы «Подобные треугольники». Решение задач по предмету Геометрия за 8 класс.
Как найти катеты если известна гипотенуза
Есть три варианта решения этой задачи. Первый — если в условиях задачи дано, что катеты равны (по сути, мы имеем прямоугольный равнобедренный треугольник). Второй — если еще дан какой-то угол (кроме угла в 45%, тогда мы имеем тот же равнобедренный треугольник и возвращаемся к первому варианту). И третий — когда известен один из катетов. Рассмотрим данные варианты подробнее.
Как найти равные катеты, при известной гипотенузе
- гипотенуза (обозначим ее буквой «c») равна х см: c=x; первый катет (обозначим его буквой «a») равен второму катету ((обозначим его буквой «b»): a=b;
В этом варианте решение задачи основывается на использовании теоремы Пифагора. Ее применяют к прямоугольным треугольникам и основной ее вариант звучит, как: «Квадрат гипотенузы равен сумме квадратов катетов». Так, как катеты у нас равны, то мы можем обозначать оба катета одним и тем же сиволом: a=b, значит — a=a.
Подставляем наши условные обозначения в теорему (с учетом вышеизложенного):
C2=a2+a2, Далее максимально упрощаем формулу:
С=√2*а — подносим обе части уравнения к квадратному кореню,
A=c/√2 — выносим искомое. Подставлем данное значение гипотенузы и получаем решение:
Как найти катеты, при известной гипотенузе и угле
- гипотенуза (обозначим ее буквой «c») равна х см: c=x; угол β равный q: β=q;
Для решения этой задачи необходимо использовать тригонометрические функции. Найболее популярны две из них:
- функция синуса — синус искомого угла равен отношению противолежащего катета к гипотенузе; функция косинуса — косинус искомого угла равен отношению прилежащего катета к гипотенузе;
Вы можете использовать любую. Я наведу пример с использованием первой. Пусть катеты у нас обозначаються символами «a» (прилежащий к углу) и «b» (противолежащий к углу). Соответственно наш угол лежит между катетом «a» и гипотенузой.
Подставляем выбранные условные обозначения в формулу:
Sinβ = b/c Выводим катет:
B=c*sinβ Подставляем наши данный и имеем один катет.
Второй катет можно найти воспользовавшись второй тригонометрической функцией, или же перейти к третьему варианту.
Как найти один катет, если известна гипотенуза и другой катет
- гипотенуза (обозначим ее буквой «c») равна х см: c=x; катет (обозначим его буквой «b») равен y см: b=y;
- размер другого катета (обозначим его буквой «a»);
В этом варианте решением задачи, как и в первом, является использование теоремы Пифагора.
Подставляем наши условные обозначения в теорему:
C2=a2+b2, Выносим необходимый катет:
A2=c2-b2 Подносим обе части уравнения к квадратному кореню:
A=√(c2-b2) Подставляем данные значения и имеем решение:
Инструкция
В вопросе так же сказано, что треугольник равнобедренный. Это означает, что Катеты равны. Для решения этого типа задач введите условные обозначения. Обозначим стороны Треугольника буквами а, а, в, где а — Катеты, а в — гипотенуза. (см. рис. 1)
С = 20 (значение выбрано произвольно для иллюстрации решения)Найти: а
2а2=с2 (это преобразование произошло потому, что в нашей конкретной задаче оба катета равны)
Подставляем известные данные:
2а2=400 (400 — это квадрат гипотенузы)
А2=200 (обе части уравнения делятся на два)
Важные теоремы
Знание теорем для рассматриваемой фигуры позволяет понять, как найти сторону, зная 2 стороны треугольника. Прежде всего применяются две базовые теоремы:
- Синусов. Как известно, синус — это тригонометрическая функция, которая вводится в прямоугольном треугольнике и определяет отношение противолежащего углу катета к гипотенузе. Теорема синусов для фигуры произвольного типа устанавливает следующее математическое взаимоотношение между отрезками и углами: a/sinA = b/sinB = c/sinC. Это означает, что вычислить длину любой стороны можно, если известен еще какой-нибудь отрезок и два угла.
- Косинусов. Как и синус, косинус тоже является тригонометрической функцией, которая определяет отношение катета прилежащего к гипотенузе прямоугольной фигуры. Теорему косинусов удобно записать в виде следующего математического выражения: c 2 = a 2 + b 2 — 2*a*b*cosC. С помощью этого равенства можно найти 3 сторону треугольника по 2 сторонам известным и углу между ними.
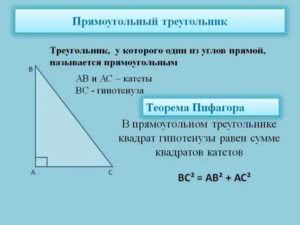
Первое выражение базируется на знаменитой теореме Пифагора, которая устанавливает связь между длинами двух катетов (меньшие стороны) и гипотенузы (большая сторона) в треугольнике с прямым углом. Если гипотенузу обозначить буквой c, тогда будет выполняться следующее равенство:
c 2 = a 2 + b 2 .
Если известные любые две стороны, то для определения третьей достаточно взять под квадратный корень соответствующую сумму или разницу квадратов.
Вторая из дополнительных теорем носит название философа Аполлония Пергского. Соответствующее ей математическое выражение выглядит так:
a 2 + b 2 = ½*c 2 + 2*Mc 2 .
Здесь Mc — это медиана, проведенная к стороне c из вершины C. Это равенство также называют в математике теоремой медианы.
Как пользоваться признаками равнобедренного треугольника при решении задач
- Если дан равнобедренный треугольный треугольник, смело проводи высоту, получай два прямоугольных треугольника и решай задачу уже про прямоугольный треугольник;
- Если дано, что два угла равны, то треугольник точно равнобедренный и можно проводить высоту и ….( Дом, который построил Джек… );
- Если оказалось, что высота разделила сторону пополам, то треугольник – равнобедренный со всеми вытекающими бонусами;
- Если оказалось, что высота разделила угол полам – тоже равнобедренный;
- Если биссектриса разделила сторону пополам или медиана разделила угол, то это тоже бывает только в равнобедренном треугольнике.
Основные понятия
Треугольник — это геометрическая фигура, которая получилось из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере плоскости, ограниченной замкнутой геометрической фигурой.
Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения
- квадратный миллиметр (мм2);
- квадратный сантиметр (см2);
- квадратный дециметр (дм2);
- квадратный метр (м2);
- квадратный километр (км2);
- гектар (га).
Свойства прямоугольного треугольника
- В прямоугольном треугольнике гипотенуза является наибольшей стороной.
- В прямоугольном треугольнике катет, лежащий напротив угла 30, равен половине гипотенузы. И обратно, если катет равен половине гипотенузы, то угол, лежащий напротив этого катета, равен 30.
Например, пусть угол А=30, а гипотенуза АВ=28 см, то катет ВС будет равен 14 см, так как лежит напротив угла А=30. Или, например, если катет ВС=6 см, а гипотенуза АВ равна 12 см, то угол А (лежащий напротив катета ВС), равен 30.
- Сумма острых углов прямоугольного треугольника равна всегда 90 градусов.
- Медиана, проведенная к гипотенузе, равна её половине.
На рисунке изображен прямоугольный треугольник АВС, где CD – медиана, проведенная к гипотенузе. По свойству – медиана CD=0,5АВ, то есть AD=DB=CD.
Тригонометрические формулы
Для нахождения длины катета прямоугольного треугольника используют простые формулы. Для их применения нужно знать значение любой из сторон и величину разворота произвольной вершины. Существует четыре способа, позволяющих найти катет с использованием тригонометрических правил:
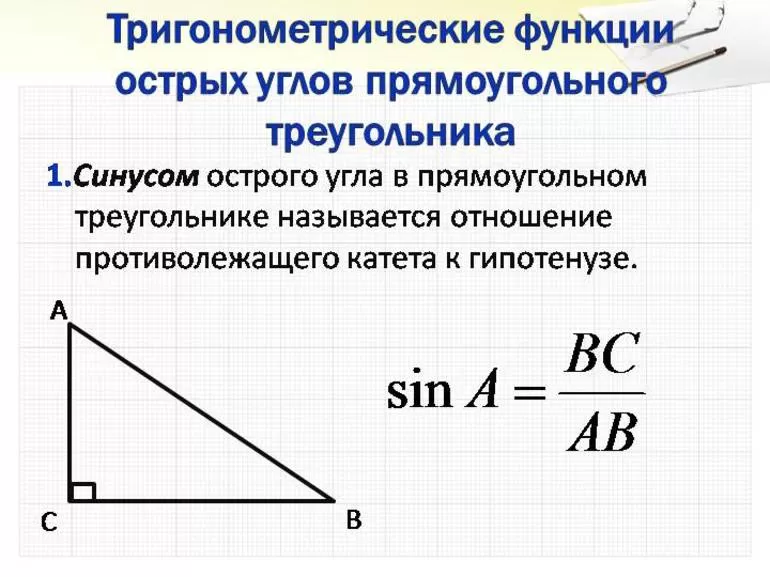
- В основе лежит аксиома, что синус находится из отношения противолежащего катета к гипотенузе. Например, пусть известно что длина гипотенузы составляет 100 сантиметров, а вершина A имеет разворот равный 30 градусам. Используя тригонометрические таблицы, можно утверждать, что синус угла A составляет ½. Учитывая преобразованное выражение, находят катет: a = 100 / 2 =50 (см). Таким образом, синус острого угла численно равен отношению одного из катетов, деленного на гипотенузу: sin A = BC/AB.
- Используется правило, что косинус в прямоугольнике представляет собой отношение прилежащего катета к прямому углу и гипотенузе: cosA = AC/AB. Например, пусть разворот вершины C равен 60 градусам, а гипотенуза равна 100 сантиметрам. Согласно тригонометрической таблице, угол в 60 градусов равен ½. Подставив это значение в формулу, можно найти значение катета: a=cos∠C*a; b=½*100=50 сантиметров.
- Тангенс угла можно вычислить, разделив значение длины противолежащего катета к прилежащему. Математическая формула этого утверждения имеет вид: tg = BC/AC. Катет многоугольника может быть найден как b = tg * a. Например, известно, что у фигуры один из углов равен 45 градусов, а длина гипотенузы составляет 100 сантиметров. Так как тангенс 45 градусов равен единице, то ответом на задачу будет: a = 1*100 = 100 сантиметров.
- Котангенс определяется из соотношения прилежащего катета к противолежащему. Фактически это величина, обратная тангенсу: ctg = AC/BC. Например, пусть разворот угла A составляет 30 градусов, а длина катета, находящегося напротив него, равняется 50 сантиметрам. Котангенс 30 градусов соответствует корню из трёх. Подставив в формулу известные данные, можно вычислить неизвестный катет: b =50√3 сантиметров.
Зная, как выглядят тригонометрические формулы и содержание двух теорем, вычислить значение катета можно будет в большинстве поставленных задач.
Признаки равнобедренного треугольника
Признак 1. Если в треугольнике две стороны равны, то треугольник является равнобедренным.
Признак 1 следует из определения 1.
Признак 2. Если в треугольнике два угла равны, то треугольник является равнобедренным.
Доказательство признака 2 смотрите в статье Соотношения между сторонами и углами треугольника (Следствие 2. Признак равнобедренного треугольника).
Признак 3. Если в треугольнике высота проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.
Доказательство. Пусть в треугольнике \( \small ABC \) \( \small AH \) является высотой и медианой (Рис.4). Тогда \( \small \angle 3=\angle4=90°, \) \( \small CH=HB. \) Треугольники \( \small AHC \) и \( \small AHB \) равны по двум сторонам и углу между ними (): \( \small AH \) − общая сторона, \( \small CH=HB, \) \( \small \angle 3=\angle4. \) Следовательно \( \small AB=AC. \)
Признак 4. Если в треугольнике высота проведенная к одной стороне совпадает с биссектрисой проведенной к этой же стороне, то треугольник является равнобедренным.
Доказательство. Пусть в треугольнике \( \small ABC \) \( \small AH \) является высотой и биссектрисой (Рис.4). Тогда \( \small \angle 3=\angle4=90°, \) \( \small \angle 1=\angle2. \) Треугольники \( \small AHC \) и \( \small AHB \) равны по стороне и прилежащим двум углам (): \( \small AH \) − общая сторона, \( \small \angle 1=\angle 2, \) \( \small \angle 3=\angle4. \) Следовательно \( \small AB=AC. \)
Признак 5. Если в треугольнике биссектриса проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.
Доказательство (Вариант 1). Пусть в треугольнике \( \small ABC \) \( \small AH \) является биссектрисой и медианой (Рис.5). Тогда
Применим теорему синусов для треугольника \( \small AHC \):
Применим теорему синусов для треугольника \( \small AHB \):
тогда, из (5), (6), (7) получим:
Следовательно \( \small \sin \angle C= \sin \angle B. \) Поскольку сумма всех углов треугольника равна 180°, то нам интересует синус углов от 0 до 180°. Учитывая это получим, что синусы углов равны в двух случаях: 1) \( \small \angle C= \angle B, \) 2) \( \small \angle C= 180° — \angle B. \) Поскольку сумма двух углов треугольника меньше 180°: \( \small \angle C + \angle B< 180° \) второй вариант исключается. Т.е. \( \small \angle C= \angle B \) и по признаку 2 треугольник является равнобедренным.
Доказательство (Вариант 2). Пусть в треугольнике \( \small ABC \) \( \small AH \) является биссектрисой и медианой, т.е. \( \small \angle 1=\angle 2, \) \( \small CH=HB \) (Рис.6). На луче \( \small AH \) отложим отрезок \( \small HD \) так, чтобы \( \small AH=HD. \) Соединим точки \( \small C \) и \( \small D. \)
Треугольники \( \small AHB \) и \( \small DHC \) равны по двум сторонам и углу между ними (). Действительно: \( \small AH=HD, \) \( \small CH=HB, \) \( \small \angle 4=\angle 5 \) (углы 4 и 5 вертикальные). Тогда \( \small AB=CD, \) \( \small \angle 6=\angle 2. \) Отсюда \( \small \angle 6=\angle 1. \) Получили, что треугольник \( \small CAD \) равнобедренный (признак 2). Тогда \( \small AC=CD. \) Но \( \small AB=CD \) и, следовательно \( \small AB=AC. \) Получили, что треугольник \( \small ABC \) равнобедренный.
Высота равнобедренного треугольника
Итак, провели высоту. Что же получилось?
Из одного равнобедренного треугольника получилось два прямоугольных.
Это уже хорошо, но так получится в любом, даже самом «кособедренном» треугольнике.
Смотри:
Тоже два прямоугольных….
Чем же отличается картинка для равнобедренного треугольника? Смотри ещё раз:
Видишь, два прямоугольных треугольника (Δ??? и Δ???) – одинаковые!
Или, как математики любят говорить? Равные!
Ну, во-первых, конечно, этим странным математикам мало просто видеть – нужно непременно доказывать. А то вдруг эти треугольники чуть-чуть разные, а мы будем считать их одинаковыми.
Но не переживай: в данном случае доказывать почти так же просто, как и видеть.
Начнём?
Площадь равнобедренного треугольника через высоту
Вычисление площади треугольника с использованием его высоты и параметров основания – самый актуальный вариант, на базе которого строятся многие другие методы решения.
У планиметрической фигуры с двумя тождественными углами и боковыми отрезками высота может рассматриваться, как медиана и биссектриса. То есть линия, проведенная из вершины, делит планиметрический объект на два эквивалентных прямоугольных треугольника.
И общая их площадь сводится к:
где:
-
b — размер основания;
-
h – высота.
Задача №1.
Требуется рассчитать S тупоугольного равнобедренного многоугольника. Его h=3 см, а длина b = 8 см.
Вычисления выглядят следующим образом:
Ответ: 12 см2.
Равнобедренный треугольник: свойства, признаки и формулы

- Свойства равнобедренного треугольника.
- Признаки равнобедренного треугольника.
- Формулы равнобедренного треугольника:
- формулы длины стороны;
- формулы длины равных сторон;
- формулы высоты, медианы, биссектрисы равнобедренного треугольника.
Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, а третья сторона — основанием.
АВ = ВС — боковые стороны
АС — основание
Свойства равнобедренного треугольника
Свойства равнобедренного треугольника выражаются через 5 теорем:
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Доказательство теоремы:
Рассмотрим равнобедренный Δ ABC с основанием АС.
Боковые стороны равны АВ = ВС,
Следовательно углы при основании ∠ BАC = ∠ BСA.
- Теорема 2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
- Теорема 3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
- Теорема 4. В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Доказательство теоремы:
- Дан Δ ABC.
- Из точки В проведем высоту BD.
- Треугольник разделился на Δ ABD и ΔCBD. Эти треугольники равны, т.к. гипотенузы и общий катет у них равны (теорема Пифагора).
- Прямые АС и BD называются перпендикуляром.
- В Δ ABD и Δ BCD∠ BАD = ∠ BСD (из Теоремы 1).
- АВ = ВС — боковые стороны равны.
- Стороны АD = СD, т.к. точка D отрезок делит пополам.
- Следовательно Δ ABD = ΔBCD.
- Биссектриса, высота и медиана это один отрезок – BD
Вывод:
- Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
- Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
- Биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и высотой.
Запомни! При решении таких задач опусти высоту на основание равнобедренного треугольника. Чтобы разделить его на два равных прямоугольных треугольника.
Теорема 5. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
Доказательство теоремы:
Дано два Δ ABC и Δ A1B1C1. Стороны AB = A1B1; BC = B1C1; AC = A1C1.
Доказательство от противного.
- Пусть треугольники не равны (а то треугольники были равны по первому признаку).
- Пусть Δ A1B1C2 = Δ ABC, у которого вершина C2 лежит в одной полуплоскости с вершиной C1 относительно прямой A1B1. По предположению вершины C1 и C2 не совпадают. Пусть D – середина отрезка C1C2. Δ A1C1C2 и Δ B1C1C2 – равнобедренные с общим основанием C1C2. Поэтому их медианы A1D и B1D являются высотами. Значит, прямые A1D и B1D перпендикулярны прямой C1C2. A1D и B1D имеют разные точки A1 и B1, следовательно, не совпадают. Но через точку D прямой C1C2 можно провести только одну перпендикулярную ей прямую.
- Отсюда пришли к противоречию и теорему доказали.
Признаки равнобедренного треугольника
- Если в треугольнике два угла равны.
- Сумма углов треугольника 180°.
- Если в треугольнике биссектриса является медианой или высотой.
- Если в треугольнике медиана является биссектрисой или высотой.
- Если в треугольнике высота является медианой или биссектрисой.
Формулы сторон равнобедренного треугольника
- b — сторона (основание)
- а — равные стороны
- a — углы при основании
- b — угол образованный равными сторонами
Формулы длины стороны (основания — b):
- b = 2a \sin( \beta /2)= a \sqrt { 2-2 \cos \beta }
- b = 2a \cos \alpha
Формулы длины равных сторон — (а):
- a=\frac { b } { 2 \sin(\beta /2) } = \frac { b } { \sqrt { 2-2 \cos \beta } }
- a=\frac { b } { 2 \cos\alpha }
Формулы высоты, медианы, биссектрисы равнобедренного треугольника
- L — высота=биссектриса=медиана
- b — сторона (основание)
- а — равные стороны
- a — углы при основании
- b — угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
- L = a sina
- L = \frac { b } { 2 } *\tg\alpha
- L = a \sqrt { (1 + \cos \beta)/2 } =a \cos (\beta)/2)
Формула высоты, биссектрисы и медианы, через стороны, (L):
L = \sqrt { a { 2 } -b { 2 } /4 }
Площадь равнобедренного треугольника
- b — сторона (основание)
- а — равные стороны
- h — высота
Формула площади треугольника через высоту h и основание b, (S):
S=\frac { 1 } { 2 } *bh
Смотри также:
Равнобедренный треугольник, свойства, признаки и формулы
- Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой по длине.
- Равнобедренный треугольник (понятие)
- Свойства равнобедренного треугольника
- Признаки равнобедренного треугольника
- Формулы равнобедренного треугольника
- Прямоугольный треугольник, равносторонний треугольник
Равнобедренный треугольник (понятие):
Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой по длине.
Две равные стороны равнобедренного треугольника называются боковыми, а третья неравная им сторона – основанием.
Рис. 1. Равнобедренный треугольник
- АВ = ВС – боковые стороны, АС – основание,
- ∠ АВС – вершинный угол, ∠ BАC и ∠ BСA – углы при основании
- По определению, каждый правильный (равносторонний) треугольник также является равнобедренным, но не каждый равнобедренный треугольник – правильным (равносторонним).
- Угол, образованный боковыми сторонами, называется вершинным углом, а углы, одной из сторон которых является основание, называются углами при основании.
- Различают следующие виды равнобедренных треугольников:
- – остроугольный – все углы острые;
- – прямоугольный – угол при вершине прямой, а при основании углы острые;
- – тупоугольный – угол при вершине тупой, а при основании углы острые;
- – равносторонний (или правильный) – все стороны равны и все углы равны.
Свойства равнобедренного треугольника:
1. В равнобедренном треугольнике углы при основании равны.
Рис. 2. Равнобедренный треугольник
∠ BАC = ∠ BСA
2. Биссектрисы, медианы и высоты, проведённые из этих углов равны между собой.
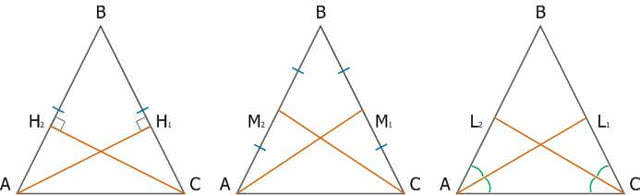
Рис. 3. Равнобедренный треугольник
АН1 = СН2 – высота, АМ1 = СМ2 – медиана, АL1 = СL2 – биссектриса, проведённые из углов при основании
3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Рис. 4. Равнобедренный треугольник
ВD – биссектриса, высота и медиана, проведенные к основанию – это один и тот же отрезок
4. Центры вписанной и описанной окружностей лежат на медиане (биссектрисе, высоте), проведенной к основанию равнобедренного треугольника.
Рис. 5. Равнобедренный треугольник
R – радиус описанной окружности, r – радиус вписанной окружности
Признаки равнобедренного треугольника:
- – если в треугольнике два угла равны, то он равнобедренный;
- – если в треугольнике биссектриса является медианой или высотой, то этот треугольник равнобедренный;
- – если в треугольнике медиана является биссектрисой или высотой, то этот треугольник равнобедренный;
- – если в треугольнике высота является медианой или биссектрисой, то этот треугольник равнобедренный.
Формулы равнобедренного треугольника:
Пусть a – длина двух равных сторон равнобедренного треугольника, b – длина основания, h – высота (биссектриса, медиана) равнобедренного треугольника, проведенная к основанию, α – углы при основании, β – вершинный угол, R – радиус описанной окружности, r – радиус вписанной окружности (см. Рис. 6, 7, 8).
Рис. 6. Равнобедренный треугольник
- Формулы длины основания (b):
- ,
- ,
- .
- Формулы длины равных сторон (а):
- .
- Формулы углов:
Рис. 7. Равнобедренный треугольник
- ,
- ,
- .
- Формулы периметра (Р) равнобедренного треугольника:
Рис. 8. Равнобедренный треугольник
- ,
- .
- Формулы площади (S) равнобедренного треугольника:
- ,
- ,
- .
- Прямоугольный треугольник
- Равнобедренный треугольник
- Равносторонний треугольник
Примечание: Фото https://www.pexels.com, https://pixabay.com
карта сайта
Равнобедренный треугольник (понятие):
Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой по длине.
Две равные стороны равнобедренного треугольника называются боковыми, а третья неравная им сторона – основанием.
Рис. 1. Равнобедренный треугольник
АВ = ВС – боковые стороны, АС – основание,
∠ АВС – вершинный угол, ∠ BАC и ∠ BСA – углы при основании
По определению, каждый правильный (равносторонний) треугольник также является равнобедренным, но не каждый равнобедренный треугольник – правильным (равносторонним).
Угол, образованный боковыми сторонами, называется вершинным углом, а углы, одной из сторон которых является основание, называются углами при основании.
Различают следующие виды равнобедренных треугольников:
– остроугольный – все углы острые;
– прямоугольный – угол при вершине прямой, а при основании углы острые;
– тупоугольный – угол при вершине тупой, а при основании углы острые;
– равносторонний (или правильный) – все стороны равны и все углы равны.






