Содержание
Формулы и свойства прямоугольного треугольника
Обозначения формул:
(см. рисунок выше)
a, b — катеты прямоугольного треугольника
c — гипотенуза
α, β — острые углы треугольника
S — площадь
h — высота, опущенная из вершины прямого угла на гипотенузу
ma— медиана, проведенная к стороне a из противолежащего угла (α)
mb — медиана, проведенная к стороне b из противолежащего угла (β)
mc — медиана, проведенная к стороне c из противолежащего угла (γ)
В прямоугольном треугольнике любой из катетов меньше гипотенузы (Формулы 1 и 2). Данное свойство является следствием теоремы Пифагора.
Косинус любого из острых углов меньше единицы (Формулы 3 и 4). Данное свойство следует из предыдущего. Так как любой из катетов меньше гипотенузы, то из соотношение катета к гипотенузе всегда меньше единицы.
Квадрат гипотенузы равен сумме квадратов катетов (теорема Пифагора). (Формула 5). Это свойство постоянно используется при решении задач.
Площадь прямоугольного треугольника равна половине произведения катетов (Формула 6)
Сумма квадратов медиан к катетам, равна пяти квадратам медианы к гипотенузе и пяти квадратам гипотенузы, деленных на четыре (Формула 7). Кроме указанной, есть еще 5 формул, поэтому рекомендуется ознакомиться также и с уроком «Медиана прямоугольного треугольника», в котором более подробно изложены свойства медианы.
Высота прямоугольного треугольника равна произведению катетов, деленному на гипотенузу (Формула 8)
Квадраты катетов обратно пропорциональны квадрату высоты, опущенной на гипотенузу (Формула 9). Данное тождество также является одним из следствий теоремы Пифагора.
Длина гипотенузы равна диаметру (двум радиусам) описанной окружности (Формула 10). Гипотенуза прямоугольного треугольника является диаметром описанной окружности. Это свойство часто используется при решении задач.
Радиус вписанной в прямоугольный треугольник окружности можно найти как половину от выражения, включающего в себя сумму катетов этого треугольника минус длину гипотенузы. Или как произведение катетов, деленное на сумму всех сторон (периметр) данного треугольника. (Формула 11) Синус угла А (α, альфа) в прямоугольном треугольнике будет равен отношению противолежащего данному углу катета к гипотенузе (по определению синуса). (Формула 12). Данное свойство используется при решении задач. Зная величины сторон, можно найти угол, который они образуют.
Косинус угла А (α, альфа) в прямоугольном треугольнике будет равен отношению прилежащего данному углу катета к гипотенузе (по определению синуса). (Формула 13)
См. также Соотношения между углами и сторонами прямоугольного треугольника изучает Тригонометрия.
Содержание главы:
Прямоугольный треугольник
Биссектриса в прямоугольном треугольнике
Высота в прямоугольном треугольнике
Высота в прямоугольном треугольнике (Часть 2)
Теорема Пифагора и ее доказательство
Применение теоремы Пифагора
Гипотенуза прямоугольного треугольника
Перпендикуляр к плоскости прямоугольного треугольника
Подобие треугольников. Использование в задачахОписание курса Прямоугольный треугольник
Признаки равнобедренного треугольника
Признак 1. Если в треугольнике две стороны равны, то треугольник является равнобедренным.
Признак 1 следует из определения 1.
Признак 2. Если в треугольнике два угла равны, то треугольник является равнобедренным.
Доказательство признака 2 смотрите в статье Соотношения между сторонами и углами треугольника (Следствие 2. Признак равнобедренного треугольника).
Признак 3. Если в треугольнике высота проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.
Доказательство. Пусть в треугольнике \( \small ABC \) \( \small AH \) является высотой и медианой (Рис.4). Тогда \( \small \angle 3=\angle4=90°, \) \( \small CH=HB. \) Треугольники \( \small AHC \) и \( \small AHB \) равны по двум сторонам и углу между ними (): \( \small AH \) − общая сторона, \( \small CH=HB, \) \( \small \angle 3=\angle4. \) Следовательно \( \small AB=AC. \)
Признак 4. Если в треугольнике высота проведенная к одной стороне совпадает с биссектрисой проведенной к этой же стороне, то треугольник является равнобедренным.
Доказательство. Пусть в треугольнике \( \small ABC \) \( \small AH \) является высотой и биссектрисой (Рис.4). Тогда \( \small \angle 3=\angle4=90°, \) \( \small \angle 1=\angle2. \) Треугольники \( \small AHC \) и \( \small AHB \) равны по стороне и прилежащим двум углам (): \( \small AH \) − общая сторона, \( \small \angle 1=\angle 2, \) \( \small \angle 3=\angle4. \) Следовательно \( \small AB=AC. \)
Признак 5. Если в треугольнике биссектриса проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.
Доказательство (Вариант 1). Пусть в треугольнике \( \small ABC \) \( \small AH \) является биссектрисой и медианой (Рис.5). Тогда
Применим теорему синусов для треугольника \( \small AHC \):
Применим теорему синусов для треугольника \( \small AHB \):
тогда, из (5), (6), (7) получим:
Следовательно \( \small \sin \angle C= \sin \angle B. \) Поскольку сумма всех углов треугольника равна 180°, то нам интересует синус углов от 0 до 180°. Учитывая это получим, что синусы углов равны в двух случаях: 1) \( \small \angle C= \angle B, \) 2) \( \small \angle C= 180° — \angle B. \) Поскольку сумма двух углов треугольника меньше 180°: \( \small \angle C + \angle B< 180° \) второй вариант исключается. Т.е. \( \small \angle C= \angle B \) и по признаку 2 треугольник является равнобедренным.
Доказательство (Вариант 2). Пусть в треугольнике \( \small ABC \) \( \small AH \) является биссектрисой и медианой, т.е. \( \small \angle 1=\angle 2, \) \( \small CH=HB \) (Рис.6). На луче \( \small AH \) отложим отрезок \( \small HD \) так, чтобы \( \small AH=HD. \) Соединим точки \( \small C \) и \( \small D. \)
Треугольники \( \small AHB \) и \( \small DHC \) равны по двум сторонам и углу между ними (). Действительно: \( \small AH=HD, \) \( \small CH=HB, \) \( \small \angle 4=\angle 5 \) (углы 4 и 5 вертикальные). Тогда \( \small AB=CD, \) \( \small \angle 6=\angle 2. \) Отсюда \( \small \angle 6=\angle 1. \) Получили, что треугольник \( \small CAD \) равнобедренный (признак 2). Тогда \( \small AC=CD. \) Но \( \small AB=CD \) и, следовательно \( \small AB=AC. \) Получили, что треугольник \( \small ABC \) равнобедренный.
Способы нахождения длины стороны
Рассматриваемая фигура обладает достаточно большим количеством геометрических свойств, которые имеют математическое выражение в виде формул. Также для нее применимы особенности тригонометрических функций и общие формулы для треугольников общего типа. Весь этот набор равенств можно использовать для нахождения любой неизвестной стороны прямоугольной фигуры. Чаще всего встречаются задачи следующего типа:
- Известны две любые стороны. Независимо от того, неизвестен один из катетов или гипотенуза, найти эту сторону легко с использованием теоремы Пифагора. Пример для катета a выглядит так: a = (c 2 — b 2 )^0,5.
- По известному острому углу и произвольной стороне. В этом случае любую из двух оставшихся неизвестных сторон треугольника легко вычислить с помощью соответствующей тригонометрической функции. Например, известен угол ∠ B и катет a, тогда: b = a*tgB, с = a/cosB.
- По катету и высоте, проведенной из прямого угла. Для решения этой задачи сначала необходимо найти острый угол исходного треугольника, который определяется с помощью тригонометрической функции синуса. Как только он станет известен, задача сводится к типу 2.
- По периметру и стороне. Эта задача имеет более сложный характер, чем описанные ранее. Решается она с помощью той же теорема Пифагора, но с применением теории квадратных уравнений.
- Наконец, самый сложный вариант задачи на нахождение произвольного катета по известным площади фигуры и высоте, которая опущена из прямого угла. Здесь также необходимо использовать теорию решения квадратных уравнений, но в дополнение к этому следует использовать замену переменных.
Пусть площадь треугольника составляет 60 см 2 , а опущенная высота из острого угла равна 8 см. Необходимо посчитать, какие длины имеют катеты и гипотенуза.
Если внимательно прочитать условие задачи, то можно увидеть, что сама высота является одним из катетов, поскольку опущена она на основание не из прямого, а из острого угла. Пусть катет a = 8 см. Сторона b вычисляется по формуле для площади:
S = ½*a*b ==>
b = 2*S/a = 2*60/8 = 15 см.
Определить гипотенузу легко по формуле Пифагора:
c = (a 2 + b2)^0,5 = (82 + 152)^0,5 = 17 см.
Общая формула
S = 0,5 * a * b⋅sin(α) , где a, b — стороны, α — угол между ними.

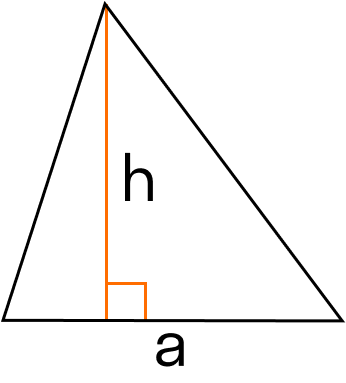
S = 0,5 * a * h, где a — основание, h — высота.
S = (a * b * c) : (4 * R), где a, b, c — стороны, R — радиус описанной окружности.

4. Площадь треугольника через вписанную окружность и стороны.
S = r * (a + b + c) : 2, где a, b, c — стороны, r — радиус вписанной окружности.

Если учитывать, что (a + b + c) : 2 — это способ поиска полупериметра. Тогда формулу можно записать следующим образом:
S = r * p, где p — полупериметр.
S = a2 : 2 * (sin(α)⋅sin(β)) : sin(180 — (α + β)), где a — сторона, α и β — прилежащие углы, γ — противолежащий угол.
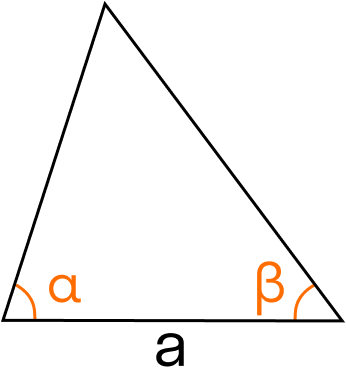
6. Формула Герона для вычисления площади треугольника.
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
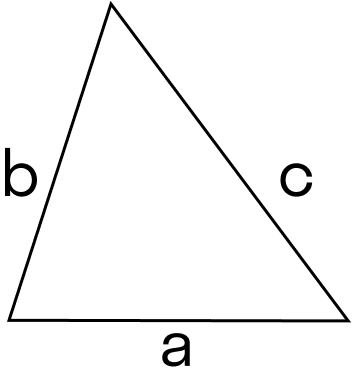
S = √ p * (p − a) * (p − b) * (p − c), где a, b, c — стороны, p — полупериметр, который можно найти по формуле: p = (a + b + c) : 2
Теорема о средней линии треугольника
Теорема о средней линии треугольника звучит так:
Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:
Докажем теорему:
-
По условию нам дано, что MA = MB, NA = NC
-
Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.
(по второму признаку подобия треугольников).
-
Так как △AMN ~ △ABC, то Следовательно, ВС = 2МN. Значит, доказано, что средняя линия равна половине основания.
-
Так как △AMN ~ △ABC, то ∠1 = ∠2 . Так как ∠1 и ∠2 — соответственные углы, то по признаку параллельности прямых MN || BC.
Параллельность средней линии и соответствующего ей основания доказана.
Теорема доказана.
Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, K, N — середины сторон AB, BC, CA соответственно. Найти периметр ΔMNK.

Соединим середины сторон треугольника ΔABC и получим его средние линии, которые образуют треугольник ΔMNK. Найдем их длины по теореме о средней линии:
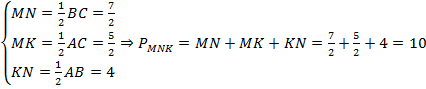
Ответ: периметр треугольника ΔMNK равен 10.
Пример 2. В прямоугольном треугольнике АВС есть две средние линии: MN и NP, равные 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.

Решение:
-
Площадь треугольника равна половине произведения основания на высоту. Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:
S = ½ × AC × BC
-
Так как MN — средняя линия, то по теореме о средней линии она равна половине катета AC:
MN = ½ × AC
Значит, AC = 2MN = 2 × 3 = 6.
-
Так как NP — средняя линия, то по теореме о средней линии она равна половине катета BC:
NP = ½ × BC
Значит, BC = 2NP = 2 × 4 = 8.
-
Тогда найдем площадь большого треугольника, используя формулу, указанную выше:
S = ½ × 6 × 8 = ½ × 48 = 24.
Ответ: площадь большого прямоугольного треугольника равна 24.
Формулы прямоугольного треугольника:
Пусть a и b – длины катетов прямоугольного треугольника, с – длина гипотенузы прямоугольного треугольника, h – высота прямоугольного треугольника, проведенная к гипотенузе (АН), R – радиус описанной окружности, r – радиус вписанной окружности (см. Рис. 9, 11, 12).
Формулы сторон прямоугольного треугольника (a, b, c) по теореме Пифагора:
c2 = a2 + b2 ,
a2 = c2 – b2 ,
b2 = c2 – a2 .
Формула радиуса вписанной окружности (r):
.
Рис. 12. Прямоугольный треугольник и вписанная окружность
Формула радиуса описанной окружности (R):
.
Формулы площади (S) прямоугольного треугольника:
.
Формулы высоты (h)прямоугольного треугольника:
.
Примечание: Фото https://www.pexels.com, https://pixabay.com
Найти что-нибудь еще?
карта сайта
Коэффициент востребованности
18 641
Понятие средней линии прямоугольного треугольника
Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.

Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.
В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.
Важное свойство
Средняя линия прямоугольного треугольника делит его на четыре прямоугольных треугольника.
Понятие треугольника
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Виды треугольников:
- Прямоугольный. Один угол прямой, то есть равен 90 градусам, два других меньше 90 градусов.
- Остроугольный. Градусная мера всех углов больше 0, но меньше 90 градусов.
- Тупоугольный. Один угол тупой, два других — острые.

Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.
Треугольник, у которого все стороны равны, называется равносторонним или правильным.
Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.
Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.
Свойства треугольников:
- В треугольнике против большего угла лежит большая сторона — и наоборот.
- Сумма углов треугольника равна 180 градусов.
- Все углы равностороннего треугольника равны 60 градусам.
- В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Признаки равенства прямоугольных треугольников
Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны (по двум катетам).
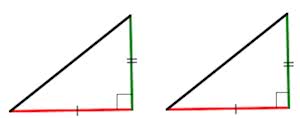
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны (по катету и острому углу).
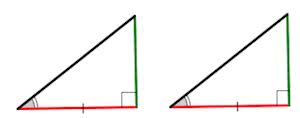 Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны (по гипотенузе и острому углу).
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны (по гипотенузе и острому углу).
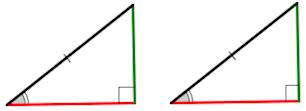
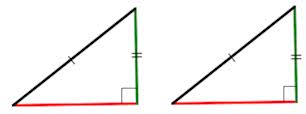
Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны (по гипотенузе и катету).
Определение тригонометрических функций.
Тригонометрические функции изначально связывались с соотношениями сторон в прямоугольном треугольнике. У них есть только один аргумент угол (1-н из острых углов треугольника).
Соотношения сторон и их связь с функциями:
- Синус — противолежащий катет к гипотенузе.
- Косинус — прилежащий катет к гипотенузе.
- Тангенс — противолежащий катет к прилежащему.
- Котангенс — прилежащий катет к противолежащему.
- Секанс — гипотенуза к прилежащему катету.
- Косеканс — гипотенуза к противолежащему катету.
Благодаря этим определениям легко вычислять значение функций для острых углов, т.е. в интервале 0 – 90° (0 – π/2 рад.).
Различные типы треугольников в зависимости от длины их сторон
Разносторонний треугольник
Мы узнаем разносторонний треугольник по трем сторонам, которые имеют разную длину. Эта треугольная форма может быть построена только с тремя разными углами. Кроме того, один из них может быть прямым углом (или углом 90 °). В общем, название «произвольный треугольник» используется для разностороннего треугольника.
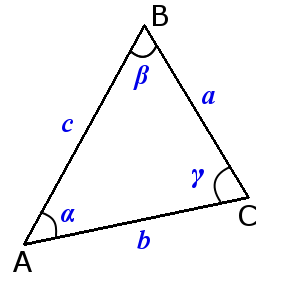
Равнобедренный треугольник
Мы говорим, что треугольник равнобедренный, если он имеет две стороны одинаковой длины и два равных угла при основании. Равнобедренный треугольник также можно узнать по тому факту, что его высота представляет его ось симметрии, его медиану и биссектрису.
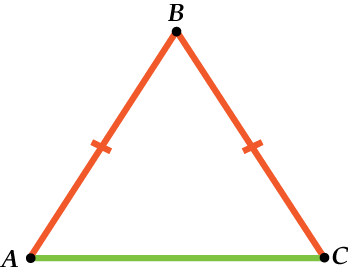
Прямоугольный треугольник
Прямоугольный треугольник обязательно имеет прямой угол. Другими словами, сумма двух других его углов должна быть равна 90°. Прямоугольный треугольник также имеет гипотенузу.
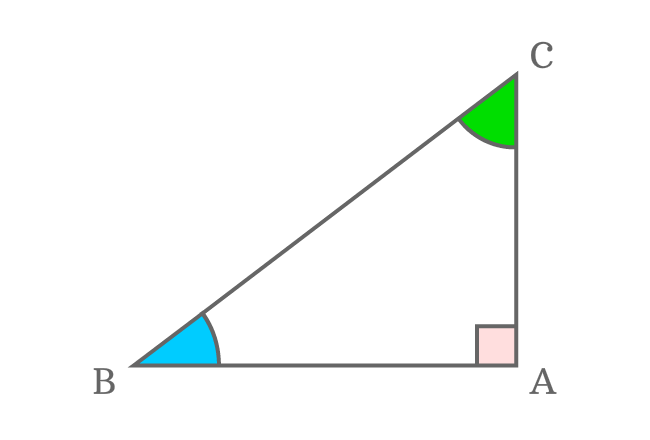
Это противоположная сторона вершине с прямым углом. Прямой треугольник может быть разносторонним (или любым), если его три стороны имеют разную длину.
Кроме того, он может быть равнобедренным в том случае, если он имеет два одинаковых катета.
Равносторонний треугольник
Треугольник называется равносторонним, если он имеет три стороны одинаковой длины. Поэтому все его углы также равны и каждый по 60°. В равностороннем треугольнике любая высота также выступает в качестве медианы и биссектрисы.
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.

Как решаем:
- Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B: - Из треугольника СМВ по теореме косинусов найдём СМ:
Ответ: СМ = √33.
Пример 2. Дан треугольник АВС, в котором a2 + b2 < c2. Доказать, что ∠C — тупой угол.

Как доказываем:
- Для доказательства нужно вспомнить теорему косинусов для угла ∠C:
- Так как a2 + b2 < c2, то cos C < 0, следовательно, ∠C — тупой.
Что и требовалось доказать.
Эта задача нам показала, что с помощью теоремы косинусов можно определить тупой угол или острый.
Если c2 = a2 + b2, то ∠C = 90°.


Второй признак равенства треугольников
Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Даны два треугольника △ABC и △A1B1C1, у которых:
AC = A1C1, ∠A = ∠A1, ∠C = ∠C1.

Докажите, что △ABC = △A1B1C1.
Доказательство:
Путем наложения △ABC на △A1B1C1, совмещаем вершину А с вершиной A1, вершины В и В1 лежат по одну сторону от А1С1.
Тогда АС совмещается с A1C1, вершина C совпадает с C1, поскольку мы знаем, что АС = A1C1.
AB накладывается на A1B1, поскольку мы знаем, что ∠A = ∠A1.
CB накладывается на C1B1, поскольку мы знаем, что ∠C = ∠C1.
Вершина B совпадает с вершиной B1.
Если АВ совмещается с А1В1, ВС совмещается с В1С1, то △ABC совмещается с △A1B1C1, значит, △ABC = △A1B1C1 .
Теорема доказана.
Признаки равенства прямоугольных треугольников:
Признаки равенства прямоугольных треугольников основаны и вытекают из общих признаков равенства треугольников.
1. Равенство по двум катетам.
Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
Рис. 2. Равенство прямоугольных треугольников по двум катетам
АВ = А1В1, АС = А1С1
2. Равенство по катету и прилежащему острому углу.
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.
Рис. 3. Равенство прямоугольных треугольников по катету и прилежащему углу
АВ = А1В1, ∠АВС = ∠А1В1С1
3. Равенство по гипотенузе и острому углу.
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Рис. 4. Равенство прямоугольных треугольников по гипотенузе и острому углу
ВС = В1С1, ∠АВС = ∠А1В1С1
4. Равенство по гипотенузе и катету.
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
Рис. 5. Равенство прямоугольных треугольников по гипотенузе и катету
ВС = В1С1, АС = А1С1
5. Равенство по катету и противолежащему острому углу.
Если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Рис. 6. Равенство прямоугольных треугольников по катету и противолежащему острому углу
АС = А1С1, ∠АВС = ∠А1В1С1
Фигура из шести элементов
Под геометрическим элементом полагают какой-либо объект, который имеет определенную меру и является составляющей частью некоторой фигуры. Например, для сферы основными образующими элементами являются радиус и центр.
Как известно, треугольник — это фигура, которая состоит из трех отрезков и такого же количества вершин. При этом все отрезки попарно пересекаются. Из определения фигуры следует, что ее образуют два типа элементов, общее количество которых составляет 6:
- сторона (3);
- вершина (3).
Дополнительные отрезки
Несмотря на всю простоту построения фигуры, она обладает большим количеством дополнительных элементов, которые ее могут определять. Среди них самыми важными являются следующие:
- Медиана — отрезок, который соединяет вершину и середину противоположной стороны. Таких отрезков в треугольнике три. Все они пересекаются в одной точке, которая является центром масс фигуры. Эта точка делит каждую медиану в отношении 2:1, начиная от вершины. Каждый из трех названных отрезков делит треугольник на две аналогичных фигуры равной площади.
- Биссектриса — отрезок, который отличается от медианы тем, что он делит пополам соответствующий угол.
- Высота — перпендикуляр, который из вершины опускается на сторону фигуры. Его удобно использовать при вычислении площади или при определении его углов через тригонометрические выражения. Для некоторых типов треугольников высота может совпадать со стороной (катет в прямоугольной фигуре).
- Радиусы вписанной и описанной окружностей. Эти замкнутые симметричные кривые можно провести для любого треугольника. Указанные радиусы однозначно определяются через стороны и углы фигуры.
- Средняя линия — это соединяющий две середины сторон отрезок. Его особенность заключается в том, что он всегда параллелен третьей стороне и равен половине ее длины.
Виды треугольников
Разработана достаточно развитая классификация рассматриваемых фигур. Главными ее пунктами являются значения углов треугольника и взаимоотношение между его отрезками. Так, если в фигуре все углы острые, то она называется остроугольной. Если же один из углов больше 90 °, то треугольник полагается тупоугольным. Чаще всего в задачах рассматривают следующие виды:
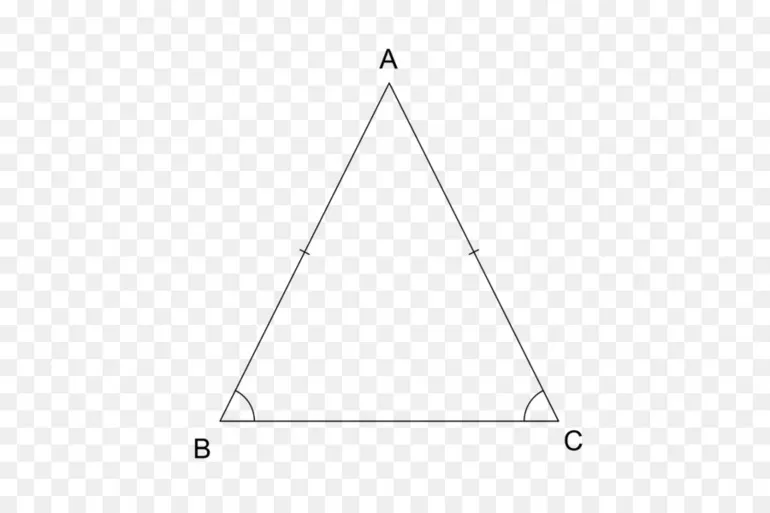
- Равнобедренный — две стороны имеют одинаковую длину. Как следствие, противолежащие им углы равны между собой.
- Равносторонний — три отрезка равны друг другу. Поэтому все углы в таком треугольнике также равны и составляют всегда по 60 °.
- Прямоугольный. Из названия следует, что он содержит один внутренний угол, который составляет 90 °. Для этого вида фигуры применима знаменитая теорема Пифагора.
Основные свойства и понятия
Треугольник является одной из самых изученных фигур в геометрии. Для него известны многие теоремы, которые с успехом используются при решении задач. Существует два основных свойства фигуры, которые следуют из характеристик евклидового пространства:
- Равенство суммы трех углов 180 °, то есть A + B + C = 180 °. Этот факт доказал еще Евклид в своем знаменитом труде «Элементы». По этой причине треугольник не может содержать больше одного прямого или тупого внутреннего угла.
- Если известны три отрезка a, b и c такие, что выполняется равенство a + b = c, то из них составить треугольник невозможно. Это фундаментальное свойство говорит о том, что для всякого типа рассматриваемой фигуры сумма длин ее двух любых сторон всегда больше длины третьей.
Помимо названных свойств, следует знать о треугольнике еще такое понятие, как подобие. Его суть состоит в том, что одна из рассматриваемых фигур является точной копией в миниатюре другой. Для подобных треугольников все углы равны попарно, а все три стороны относятся соответственно попарно друг к другу с одним и тем же коэффициентом подобия.
Еще одной полезной характеристикой рассматриваемой фигуры является ее качество (CT). Вычисляется оно по следующей формуле:
CT = (a + b — c)*(b + c — a)*(c + a — b)/(a*b*c).
Величина CT лежит в пределах от 0 до 1. Она показывает степень близости фигуры к равностороннему, то есть к наиболее симметричному объекту. Если CT < 0,5, то треугольник считается вырожденным (один из его углов будет тупым, причем чем меньше CT, тем больше величина этого угла), если же CT > 0,5, то фигура характеризуется, как имеющая хорошее качество.
Онлайн калькулятор
Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Катет a = Катет b = Гипотенуза c =
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:
c² = a² + b²
следовательно: c = √a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √3² + 4² = √9 + 16 = √25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Катет (a или b) = Прилежащий угол (β или α) = Гипотенуза c =
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
c = a/cos(β) = b/cos(α)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Катет (a или b) = Противолежащий угол (α или β) = Гипотенуза c =
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
c = a/sin(α) = b/sin(β)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.
Найти катет
Найти катет по гипотенузе и катету
Гипотенуза c = Катет (известный) = Катет (искомый) =
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
a = √c² — b²
b = √c² — a²
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √5² — 4² = √25 — 16 = √9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Гипотенуза c = Угол (прилежащий катету) = °Катет =
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
a = c ⋅ cos(β)
b = c ⋅ cos(α)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Гипотенуза c = Угол (противолежащий катету) = °Катет =
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
a = c ⋅ sin(α)
b = c ⋅ sin(β)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Катет (известный) = Угол (прилежащий известному катету) = °Катет (искомый) =
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
a = b ⋅ tg(α)
b = a ⋅ tg(β)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Катет (известный) = Угол (противолежащий известному катету) = °Катет (искомый) =
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
a = b / tg(β)
b = a / tg(α)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
a = 3 / tg(35) ≈ 3 / 0.7 ≈ 4.28 см
Первый признак равенства треугольников
Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.
Давайте рассмотрим три признака равенства треугольников.
Теорема 1. Равенство треугольников по двум сторонам и углу между ними.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Даны два треугольника △ABC и △A1B1C1, у которых AC = A1C1, AB = A1B1, ∠A = ∠A1.

Докажите, что △ABC = △A1B1C1.
Доказательство:
При наложении △A1B1C1 на △ABC вершина A1 совмещается с вершиной A, и сторона A1B1 накладывается на сторону AB, AC — на сторону A1C1.
Сторона A1B1 совмещается со стороной AB, вершина B совпадает с вершиной B1, сторона A1С1 совмещается со стороной AС, вершина C совпадает с вершиной C1.
Значит, происходит совмещение вершин В и В1, С и С1.
B1C1 = BC, следовательно, △ABC совмещается с △A1B1C, значит, △ABC = △A1B1C1.
Теорема доказана.
Важно!
Первый признак используют при доказательстве второго и третьего признаков равенства треугольников.
Познавайте математику вместе с нашими лучшими преподавателями на занятиях по математике для учеников с 1 до 11 класса!
Формулировка и доказательство теоремы косинусов
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Формула Теоремы Пифагора:
a2> + b2> = c2>, где a, b — катеты, с — гипотенуза.

Из формулы следует: a2 = c2 — b2
К полученному выражению прибавим и отнимем квадрат второго катета:
Но так как b = c * cos α, то
Эту формулу мы получили для катетов в прямоугольном треугольнике, но аналогичная связь между стороной а и косинусом противолежащего угла справедлива и для произвольного треугольника.
|
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними. |
Формула теоремы косинусов:
a2 = b2 + c2 — 2bc cos α

В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:
BC2 = (x2 — x1)2 + (y2 — y1)2

В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
BC2 = a2 = (b cos α — c)2 + b2sin2α = b2cos2α + b2sin2α — 2bc cos α + c2 = b2(cos2α + sin2α) — 2bc cos α + c2
cos2α + sin2α = 1 — основное тригонометрическое тождество.
b2(cos2α + sin2α) — 2bc cos α + c2 = b2 + c2 — 2bc cos α
Что и требовалось доказать.
Следствие из теоремы косинусов: теорему косинусов также можно использовать для определения косинуса угла треугольника:
- Когда b2 + c2 — a2 > 0, угол α будет острым.
- Когда b2 + c2 — a2 = 0, угол α будет прямым.
- Когда b2 + c2 — a2 < 0, угол α будет тупым.
Запоминаем
Когда угол α прямой, то теорема косинусов превращаеся в теорему Пифагора.
Сформулируем еще одно доказательство теоремы косинусов.
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
- AD = b * cos α,
- DB = c – b * cos α.

Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
- h2 = b2 — (b * cos α)2
- h2 = a2 — (c – b * cos α)2
Приравниваем правые части уравнений:
b2 — (b * cos α)2 = a2 — (c — b * cos α)2
либо
a2 = b2 + c2 — 2bc * cos α
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определим стороны b и c:
- b2 = a2 + c2 — 2ac * cos β;
- c2 = a2 + b2 — 2ab * cos γ.

Вывод формул для площади равностороннего треугольника
Утверждение 7.
- Если a – сторона равностороннего треугольника, то его площадь
Если h – равностороннего треугольника, то его площадь
Если r – радиус , то его площадь
Если R – радиус около равностороннего треугольника окружности, то его площадь
Доказательство.
- Рассмотрим рисунок 7.
Рис. 7
В силу утверждения 2
Рассмотрим рисунок 8.
Рис. 8
Поскольку
то
Рассмотрим рисунок 9.
Рис. 9
Поскольку у равностороннего треугольника , то . Следовательно,
Рассмотрим рисунок 10.
Рис. 10
Поскольку у равностороннего треугольника центр описанной окружности совпадает с точкой пересечения медиан, высот и биссектрис, то выполнено равенство Следовательно,
Доказательство утверждения 7 завершено.






