Длина окружности круга

Введение

Как вы знаете, многие предметы имеют форму круга. Чем это обусловлено?

Возьмем, к примеру, колесо. Понятно, что круглое колесо катится гораздо лучше, чем, например, квадратное. Или, скажем, стакан круглой формы удобнее держать в руке, чем стакан прямоугольной формы. Поэтому в какой-то момент человечество стало использовать круглые предметы. Но если вы используете круглые предметы, нужно научиться их измерять. Например, вам нужно знать длину окружности стакана, чтобы понять, сколько материала пойдет на его изготовление, или вам нужно знать площадь колеса, чтобы, например, определять, какой должен быть объем исходных материалов, чтобы его сделать.

Поэтому сегодня мы обсудим, как же учились находить длину окружности и площадь круга, и решим некоторые задачи, связанные с этим.

Второй метод определения радиуса дуги (метод последовательных приближений)

Итак продолжим рассмотрение имеющейся ситуации.

Так как нам все равно необходимо найти центр окружности, то для начала мы из точек, соответствующих началу и концу дуги, проведем как минимум две дуги произвольного радиуса. Через пересечение этих дуг будет проходить прямая, на которой и находится центр искомой окружности.

Теперь нужно соединить пересечение дуг с серединой хорды. Впрочем, если мы из указанных точек проведем не по одной дуге, а по две, то данная прямая будет проходить через пересечение этих дуг и тогда искать середину хорды вовсе не обязательно.

Ну а дальше все просто: измеряем расстояние от пересечения дуг до начала (или конца) рассматриваемой дуги, а затем расстояние от пересечения дуг до точки, соответствующей высоте сегмента.

Если расстояние от пересечения дуг до начала или конца рассматриваемой дуги больше, чем расстояние от пересечения дуг до точки, соответствующей высоте сегмента, то значит центр рассматриваемой дуги находится ниже на прямой, проведенной через пересечение дуг и середину хорды. Если меньше — то искомый центр дуги выше на прямой.

Исходя из этого на прямой принимается следующая точка, предположительно соответствующая центру дуги, и от нее производятся те же измерения. Затем принимается следующая точка и измерения повторяются. С каждой новой точкой разница измерений будет все меньше.

Вот собственно и все. Не смотря на столь пространное и мудреное описание, для определения радиуса дуги таким способом с точностью до 1 мм достаточно 1-2 минут.

Теоретически это выглядит примерно так:

Рисунок 463.2. Определение центра дуги методом последовательных приближений.

А на практике примерно так:

Фотография 463.1. Разметка заготовки сложной формы с разными радиусами.

Тут только добавлю, что иногда приходится находить и чертить несколько радиусов, потому на фотографии так много всего и намешано.

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Для Украины — номер гривневой карты (Приватбанк) 5168 7422 4128 9630

R = H/(1 — cos(a/2)) Радиус прямо пропорционален H. Как так?

Я достаточно подробно ответил на ваш вопрос в статье «Расчет арочной перемычки», где вы задали подобный вопрос.

Если угол не нужен для дальнейших расчетов, радиус находится проще — без тригонометрических функций и даже можно без калькулятора — на бумажке. R = L^2/(8*H) + H/2

Сначала термины: Отрезок, соединяющий концы дуги называется хордой (a), а высота сегмента (перпендикуляр из середины хорды) — стрелкой (h). Теорема Пифагора: Квадрат гипотенузы равен сумме квадратов катетов. То есть R^2=(R-h)^2+(a/2)^2. А что касается нахождения центра, то перпендикуляры к серединам хорд пересекаются в центре!

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Источник

Углы между хордами и секущими

До этого мы рассматривали простые углы в окруж-ти, вершины которых лежали либо на самой окруж-ти, либо в ее центре. Однако иногда хорды и секущие пересекаются в другой точке, либо внутри, либо вне окруж-ти. Рассмотрим подобные задачи.

Более прост случай, когда необходимо найти угол между двумя пересекающимися хордами. Пусть хорды при пересечении образовали дуги ⋃AВ и ⋃СD величиной α и β. Каков угол между ними?

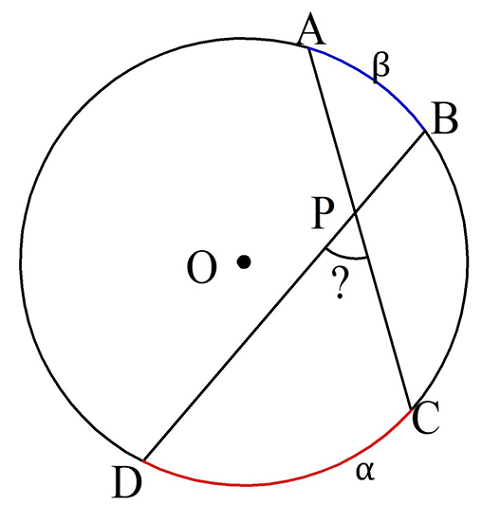
Проведем ещё одну хорду АD. В результате получим вписанные ∠САD и ∠ADB, которые будут равны половинам от соответствующих дуг, то есть α/2 и β/2. Интересующий нас ∠СPD оказывается внешним для ∆APD, и потому равен сумме двух углов в ∆APD (тех, которые с ним не смежны), то есть он составляет величину α/2 + β/2:

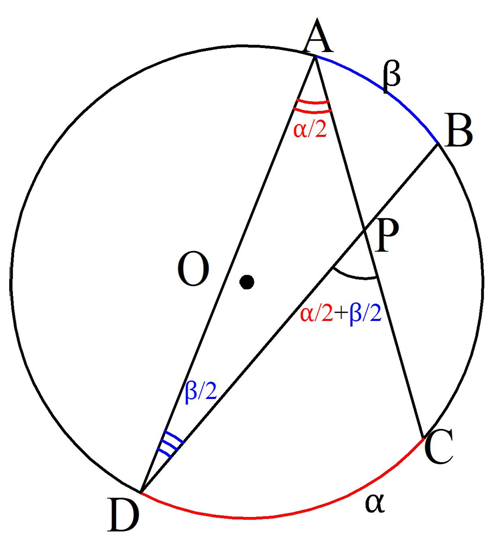
Величину α/2 + β/2 можно записать и иначе, вынеся множитель 1/2 за скобки:

α/2 + β/2 = (α + β)/2

Эту величину можно назвать полусуммой дуг, на которые опирается интересующий нас угол.

Задание. Найдите ∠МКВ на рисунке:

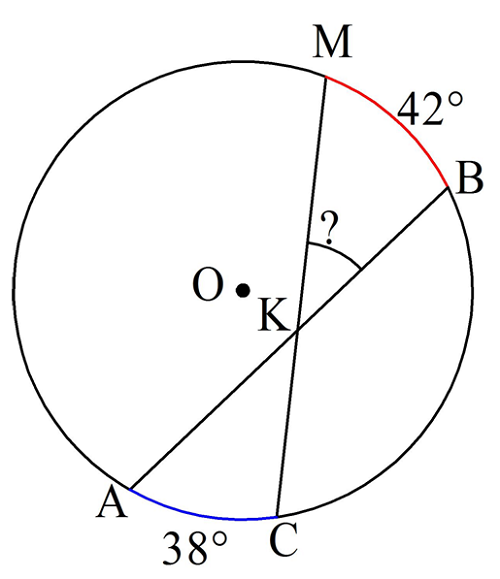
Решение. Интересующий нас угол опирается на хорды величиной 38° и 42°. Значит, он равен половине от их суммы:

∠MKB = (42° + 38°)/2 = 80°/2 = 40°

Ответ: 40°.

В более сложном случае необходимо найти угол между секущими, которые пересекаются вне окруж-ти. При этом известны дуги, образованные этими секущими:

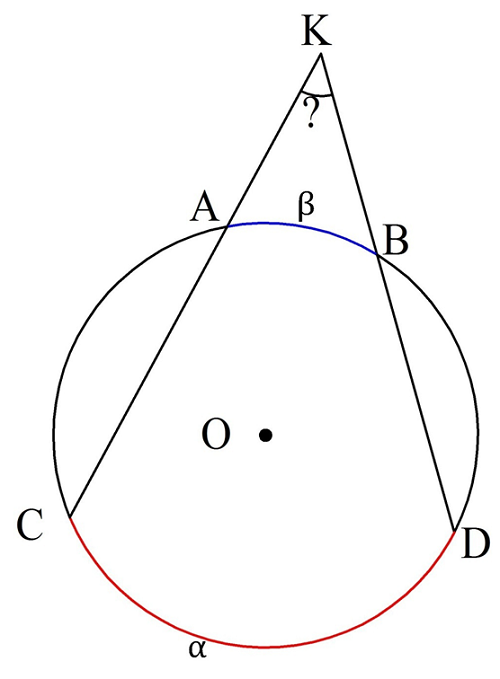
Снова проведем хорду АD, чтобы у нас получились два вписанных угла, ∠ADB и ∠СAD, которые соответственно будут иметь величину β/2 и α/2:

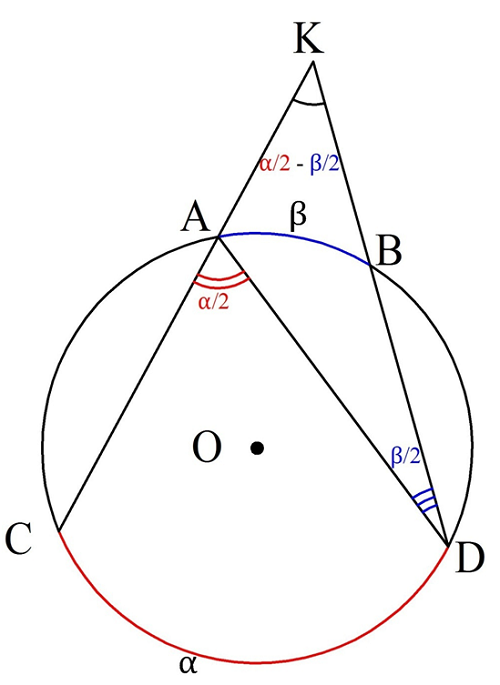
Теперь уже ∠САD оказывается внешним для ∆ADK, а потому он является суммой двух других углов:

В итоге получили, что угол между секущими составляет половину от разности дуг, которые они отсекают от окруж-ти.

Задание. Найдите на рисунке величину∠К, если ⋃AВ и ⋃СD соответственно равны 42° и 130°:

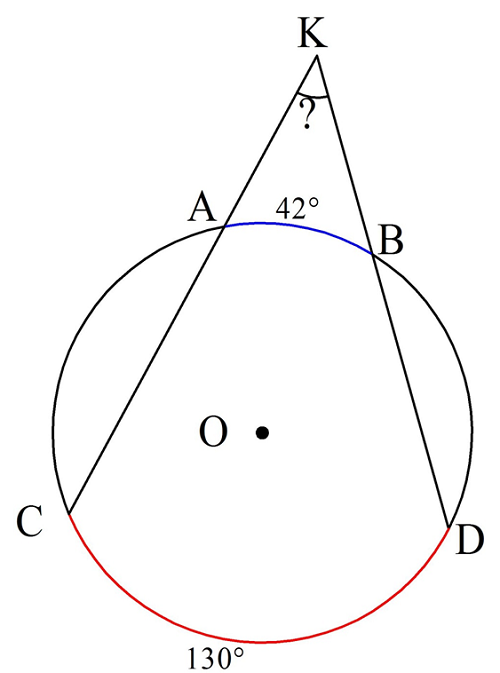
Решение. В этой задаче просто используем доказанную теорему об углах между секущими. Искомый угол составляет половину от разности дуг, заключенных между секущими:

∠K = (130° — 42°):2 = 88°/2 = 44°

Ответ: 44°.

Окружность (сравнение с другими фигурами)

У круга есть одна подруга,

Знакома всем её наружность,

Она идет по краю круга

И называется окружность.

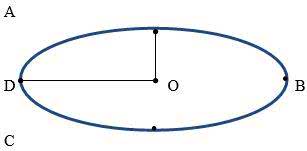
Если рассмотреть рисунки 1-6 в таблице 1 и определить те линии, которые являются незамкнутыми, увидим, что это рисунки 1 и 2. Из оставшихся фигур видно, что рисунки 3 и 6 – это ломаные замкнутые линии. А рисунки 4 – это овал, и 5 – это окружность.

Таблица 1. Линии

Давайте сравним между собой овал и окружность (рис. 7–8). А данные о сравнении занесём в таблицу 2.

Таблица 2. Сравнение овала и окружности

Окружность – это замкнутая кривая линия с точкой  в середине, которая называется центром. Расстояния от центра до линии окружности одинаковые.

Необходимость расчётов

Геометрическими формулами, связанными с подсчетом площади сектора, объема сегмента и периметра полукруга, следует виртуозно владеть людям, связавшим свою жизнь со строительством или благоустройством территорий. Чтобы обновить после зимы элементы архитектуры городского парка и закрасить дефекты абстрактных скульптур, не нужно вспоминать сложные уравнения, достаточно применить знание геометрических формул.

К примеру, для правильного нахождения веса декоративного камня, предназначенного для окантовки части клумбы, нужно уметь быстро посчитать размер полуокружности на поверхности ландшафта. Затем необходимо определиться с ценой и принять решение, какой камень можно покупать с учетом сметы. Аналогичная задача возникает при строительстве альпийской горки. Тяжесть камня обеспечит круговую укладку, это свойство позволит высадить декоративные растения в запланированных местах сечения, придав конструкции форму трапеции.

Что представляет собой часть клумбы? Это сектор геометрической фигуры. Внешняя его часть — окантовка клумбы — чаще всего представляет собой дугу окружности. Существует две методики вычисления этой величины:

• градусная (с привязкой к центральному углу);
• по формуле Гюйгенса (с использованием хорды).

Для удобства рассмотрим пример с двумя точками A и B, расположенными на окружности на небольшом расстоянии друг от друга. Они делят её на 2 части — большую и меньшую. Каждая из них называется дугой окружности.

Шар, сфера и их части

Введем следующие определения, связанные с шаром, сферой и их частями.

Определение 1. Сферой с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O равно r (рис. 1).

Определение 2. Шаром с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O не превосходит r (рис. 1).

Рис.1

Таким образом, сфера с центром в точке O и радиусом r является поверхностью шара с центром в точке O и радиусом r.

Замечание. Радиусом сферы (радиусом шара) называют отрезок, соединяющий любую точку сферы с центром сферы. Длину этого отрезка также часто называют радиусом сферы (радиусом шара).

Определение 3. Сферическим поясом (шаровым поясом) называют часть сферы, заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).

Определение 4. Шаровым слоем называют часть шара, заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).

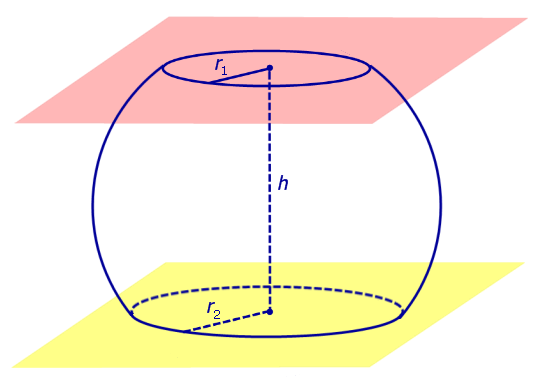
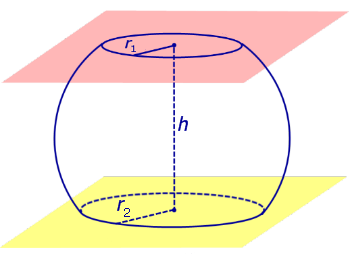
Рис.2

Окружности, ограничивающие сферический пояс, называют основаниями сферического пояса.

Расстояние между плоскостями Расстояние между плоскостями оснований сферического пояса называют высотой сферического пояса.

Из определений 3 и 4 следует, что шаровой слой ограничен сферическим поясом и двумя кругами, плоскости которых параллельны параллельны между собой. Эти круги называют основаниями шарового слоя.

Высотой шарового слоя называют расстояние между плоскостями расстояние между плоскостями оснований шарового слоя.

Определение 5. Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость (рис. 3).

Определение 6. Шаровым сегментом называют каждую из двух частей, на которые делит шар пересекающая ее плоскость (рис. 3).

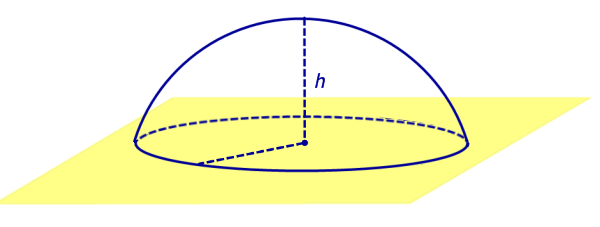
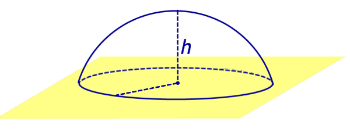
Рис.3

Из определений 3 и 5 следут, что сферический сегмент представляет собой сферический пояс, у которого одна из плоскостей оснований касается сферы (рис. 4). Высоту такого сферического пояса и называют высотой сферического сегмента.

Соответственно, шаровой сегмент – это шаровой слой, у которого одна из плоскостей оснований касается шара (рис. 4). Высоту такого шарового слоя называют высотой шарового сегмента.

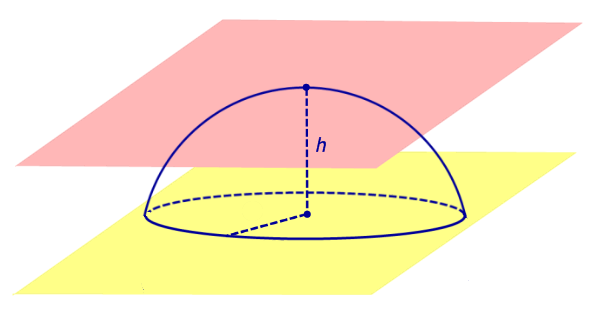
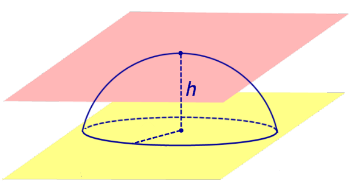
Рис.4

По той же причине всю сферу можно рассматривать как сферический пояс, у которого обе плоскости оснований касаются сферы (рис. 5). Соответственно, весь шар – это шаровой слой, у которого обе плоскости оснований касаются шара (рис. 5).

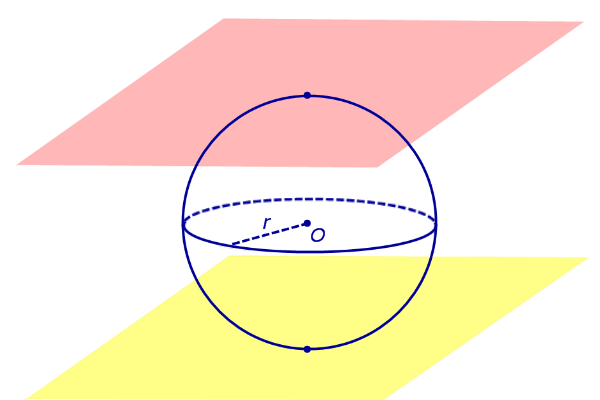
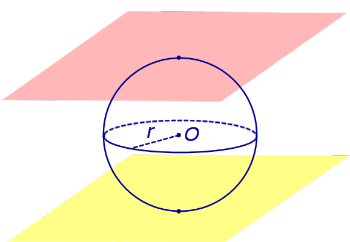
Рис.5

Определение 7. Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы (рис. 6).

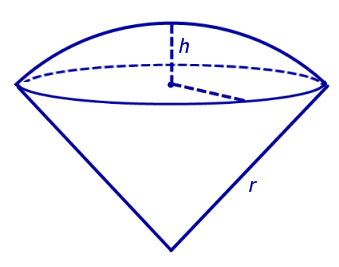
Рис.6

Высотой шарового сектора называют высоту его сферического сегмента.

Замечание. Шаровой сектор состоит из шарового сегмента и конуса с общим основанием. Вершиной конуса является центр сферы.

Основные свойства сферы и шара

1. Все точки сферы одинаково удалены от центра.
2. Любое сечение сферы плоскостью является окружностью.
3. Любое сечение шара плоскостью есть кругом.
4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.
5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.
6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.
7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.
8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются, а в плоскости пересечения образуется круг.

Как найти площадь круга через длину окружности

Для начала вспомним, как вычисляется длина окружности. Здесь, как и в других формулах для круга и окружности используется постоянная π. Нужно запомнить, что в математике и физике этот символ является непременным участником всех вычислений, связанных с кругом, окружностью, циклическими процессами, движением по дуге. В частности, длину окружности находим по формулам L=2 πR, или L= πD. Используя их, находим:

R=L/2 π; (1)

D=Lπ.  (2)

Используя запись 1 в формуле S = π∙r2 получаем:

S = π(L/2 π)2 = L/4 π.

Аналогичный результат получим, используя формулу 2.

Как вычислить площадь круга, описанного вокруг правильного многоугольника

В каждый круг легко вписать любой правильный многоугольник. Рассмотрим случаи с самыми простыми фигурами. Если в круг вписан квадрат, то формула будет выглядеть так:

S=​2​​π⋅a​2​​​​/2, где а – сторона квадрата.

Если в круг вписан равносторонний (правильный) треугольник, то формула будет выглядеть так:

S=π⋅​​​a​2/3.

Если в равностороннем треугольнике неизвестна длина стороны, но известна высота, то используем формулу:

S=π⋅(​​​2⋅h​​/3)​2​​.

Если треугольники неправильные, например, равнобедренные или разносторонние, то формулы получаются сложнее. Например, для вычисления площади по данным равнобедренного треугольника используется формула:

S=π⋅(​ a4/4⋅a​2​​−b​2​​​​)

В случае прямоугольного треугольника, мы используем формулу:

S=​π/4​​⋅(a​2​​+b​2)​​.

Если круг описан вокруг равнобедренной трапеции, то рассчитать площадь можно по более сложной формуле:

S=π⋅( a⋅d⋅c/​4⋅√​p⋅(p−a)⋅(p−d)⋅(p−c)​​​​​).

Как видим, задачу вычисления площади круга можно решить при помощи готовых формул, рассчитанных практически для любого случая, используя вписанные или описанные простые геометрические фигуры. Приведем еще несколько из готовых формул, на этот раз, для фигур, внутри которых находится круг неизвестного радиуса:

S=π⋅​​​a​2​​/12 – для равностороннего треугольника;

S=π⋅​​​b​2/4​​​​⋅(tg​α​/2​​​​)​2​​ — для равнобедренной трапеции;

S=π⋅(​а/2​​)​2​​=​π⋅а​2/4​​ — для квадрата.

Учитывая небольшой объем статьи, все формулы приводим без доказательств, как руководство для практического использования при решении геометрических или технических задач.

Часто возникает проблема определения площади полукруга. Это можно сделать очень просто, вычислив площадь полного круга и разделив ее на 2. Если использовать формулу, то выглядеть это будет так:

S = π∙r2/2, или

S= π∙ D2/4/2 = S= π∙ D2/8.

Для решения практических задач сложно пользоваться формулами, да и времени для этого найти не всегда получается. Лучше всего воспользоваться онлайн-калькуляторами на специализированных сайтах

Здесь важно правильно замерить нужные параметры в требуемых единицах. Нот для учеников и студентов такие сервисы не подходят — легкое получение готового результата отучает мыслить самостоятельно и никак не углубляет знаний

Формулы

Чтобы посчитать периметр круга, необходимо знать его диаметр (D) или радиус (R), который равняется D, деленному на 2.

Как вычислить длину окружности через радиус? Это делается по простой формуле:

L = 2πR,

где L – искомая величина,

π – число пи, примерно равное 3,1413926.

Обычно для нахождения нужной величины достаточно использовать π до второго знака, то есть 3,14, это обеспечит нужную точность. На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.

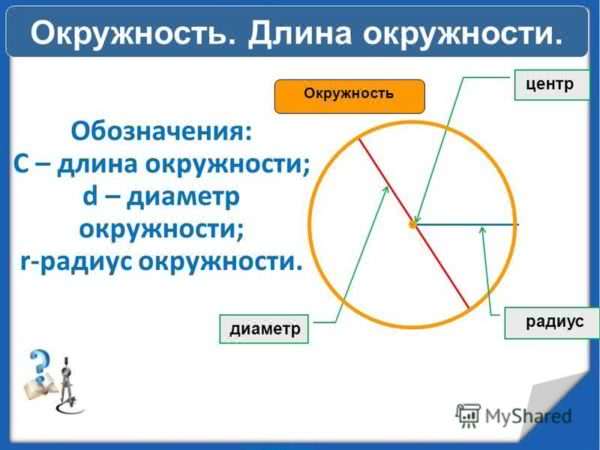Обозначения

Для нахождения через диаметр существует следующая формула:

L = πD.

Если L уже известно, можно легко узнать радиус или диаметр. Для этого L нужно поделить на 2π или на π соответственно.

Если уже дана площадь круга, нужно понимать, как найти длину окружности по этим данным. Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда

L = 2πR = 2π√(S/π) = 2√(Sπ).

Вычислить площадь через L также несложно: S = πR2 = π(L/(2π))2 = L2/(4π)

Резюмируя, можно сказать, что существует три основных формулы:

• через радиус – L = 2πR,
• через диаметр – L = πD,
• через площадь круга – L = 2√(Sπ).

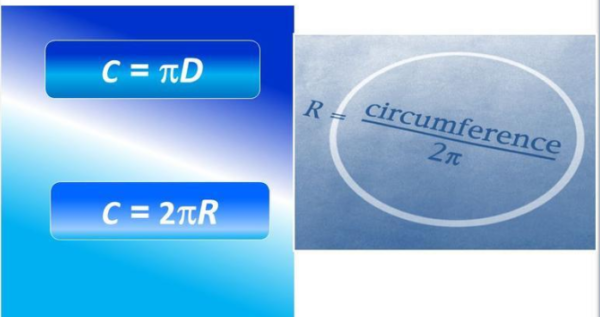Формулы

Что такое шар?

В стереометрии есть большой раздел, который называется фигуры вращения. Об этом редко говорят в школе, но плоские фигуры можно вращать вокруг какой-либо оси или точки. Так получаются объемные фигуры.

Например, цилиндр образован вращением прямоугольника или квадрата. Поэтому, если рассечь цилиндр плоскостью, то сечение примет форму того самого квадрата или прямоугольника, который вращали, чтобы получить фигуру.

Так же и шар образован вращением. Как не трудно догадаться, основной для шара послужил круг. Причем сразу стоит сказать, что именно круг, а не окружность.

Следует понимать, что круг и окружность разные фигуры. Так окружность представляет собой набор точек равноудаленных от центра. Переводя на более простой язык окружность – это сама линия и центр окружности. А круг включает в себя и все внутреннее пространство. У окружности не может быть площади.

То есть, шар имеет какое-то внутренне заполненное пространство. Интересно, что сфера так же имеет пространство внутри, только условно полое.

Формулы для вычисления радиуса

1. 1

   Вычислите радиус по диаметру. Радиус равен половине диаметра, поэтому используйте формулу г = D/2. Эта такая же формула, которая используется при вычислении радиуса и диаметра круга.

   Например, дан шар с диаметром 16 см. Радиус этого шара: r = 16/2 = 8 см. Если диаметр равен 42 см, то радиус равен 21 см (42/2=21).

2. 2

   Вычислите радиус по длине окружности. Используйте формулу: r = C/2π. Так как длина окружности C = πD = 2πr, то разделите формулу для вычисления длины окружности на 2π и получите формулу для нахождения радиуса.

   • Например, дан шар с длиной окружности 20 см. Радиус этого шара: r = 20/2π = 3,183 см.
   • Такая же формула используется при вычислении радиуса и длины окружности круга.

3. 3

   Вычислите радиус по объему шара. Используйте формулу: r = ((V/π)(3/4))1/3. Объем шара вычисляется по формуле V = (4/3)πr3. Обособив r на одной стороне уравнения, вы получите формулу ((V/π)(3/4))3 = г, то есть для вычисления радиуса объем шара делим на π, результат умножаем на 3/4, а полученный результат возводим в степень 1/3 (или извлекаем кубический корень).

   • Например, дан шар с объемом 100 см3. Радиус этого шара вычисляется так:
     • ((V/π)(3/4))1/3 = r
     • ((100/π)(3/4))1/3 = r
     • ((31,83)(3/4))1/3 = r
     • (23,87)1/3 = r
     • 2,88 см = r

4. 4

   Вычислите радиус по площади поверхности. Используйте формулу: г = √(A/(4 π)). Площадь поверхности шара вычисляется по формуле А = 4πr2. Обособив r на одной стороне уравнения, вы получите формулу √(A/(4π)) = r, то есть, чтобы вычислить радиус, нужно извлечь квадратный корень из площади поверхности, деленной на 4π. Вместо того чтобы извлекать корень, выражение (A/(4π)) можно возвести в степень 1/2.

   • Например, дан шар с площадью поверхности 1200 см3. Радиус этого шара вычисляется так:
     • √(A/(4π)) = r
     • √(1200/(4π)) = r
     • √(300/(π)) = r
     • √(95,49) = r
     • 9,77 см = r

Круглые предметы в истории человеческой жизни

Первое изделие круглой формы, которое изобрёл человек — это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.

Форму колеса имеет гончарный круг, большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве — рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах. Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.

https://youtube.com/watch?v=r7Zsq89ClDI

Способы расчета

Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.

Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.

При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.

Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).

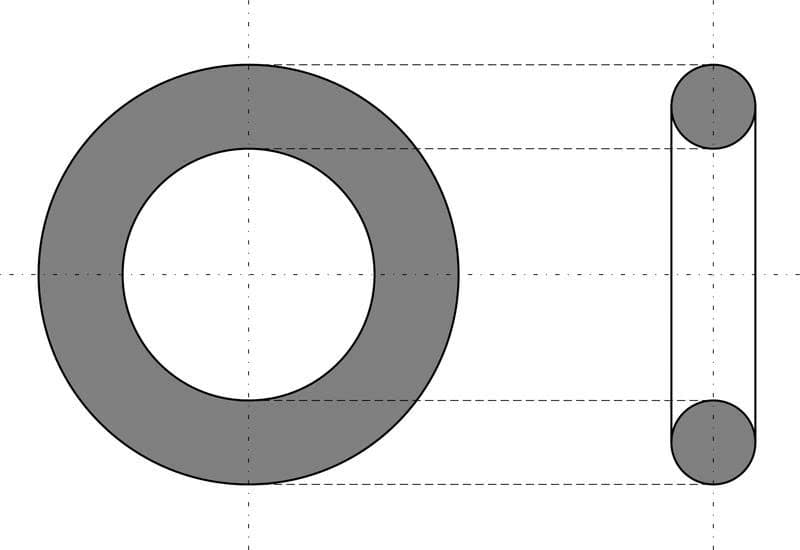
Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:

1. Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
2. Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
3. Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.

Основные формулы для вычислений

Параметры используются в формулах вычислений величин окружности:

• длину фигуры вычисляют умножением диаметра на число π и записывают таким образом: C = π*D.
• Величина диаметра в два раза превышает длину радиуса. Иной способ вычисления радиуса — необходимо разделить длину круга на удвоенное π: R = C/(2* π) = D/2.
• Диаметр рассчитывается с помощью радиуса или делением длины окружности на число π. Формула нахождения диаметра: D = C/π = 2*R.
• Площадь круга, ограниченного окружностью, можно найти двумя способами: через радиус или диаметр. По формуле площадь равна четвёртой части произведения числа π и диаметра в квадрате или радиусу в квадрате, умноженному на π: S = π*R2 = π*D2/4.

Диаметр в формулах вычисления

В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.

Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него. В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.

Расчёты по радиусу

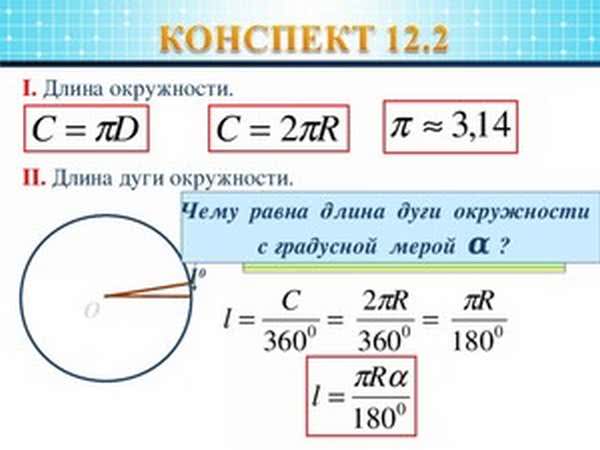Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С — длина, r — радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.

Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?

Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы. Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.

Подручные способы вычисления

Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:

• При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.
• Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.
• Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.

Примеры на вычисление длины окружности

Пример 1

Дана окружность с радиусом 2 сантиметра. Чему равна ее длина?

Решение:

Ответ: 12,56 см.

Как видите, тут мы использовали знак приблизительного равенства.

Пример 2

Диаметр окружности равен 3 см, чему равна длина этой окружности?

Решение:

Ответ: 9,42 см.

Можно было записать ответ в виде: .

В этом случае мы можем поставить знак равенства, ведь значение абсолютно точное. Другой вопрос, что для практических целей оно не совсем удобно. Но так как математика – точная наука, то точным ответом будет .

Между прочим, формулу  можно преобразовать. Если вспомнить, что диаметр – это удвоенный радиус, мы можем записать формулу в виде

Или:

Характеристики фигуры

Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.

В пределах окружности имеются точки Х такие, что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.

Основные термины окружности

Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда. Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками, проходящее через центр фигуры.

Свойства радиуса

В отношении радиуса действуют несколько важных правил:

1. Радиус составляет половину диаметра. Это мы продемонстрировали только что.

2. У окружности может быть сколько угодно радиусов. Но все они будут равны по длине между собой.

3. Если в точке пересечения радиуса с поверхностью окружности провести касательную, то эти две линии будут пересекаться под прямым углом. Доказательство этой теоремы наглядно приводится на следующем рисунке.

4. Напомним, хордой называется любой отрезок, который проходит через две точки на поверхности окружности, но не через центр. Этим она принципиально отличается от диаметра.

Заключение

Сегодня мы вспомнили, что такое окружность и что такое круг. Поняли, как люди научились считать длину окружности и площадь круга хотя бы приблизительно. Узнали, по каким формулам можно найти длину окружности и площадь круга, и научились этими формулами пользоваться.

Обратите внимание, что можно решать и обратные задачи, то есть находить радиус (диаметр) по заданной длине окружности или площади круга. Список литературы. Список литературы

Список литературы

1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. – М.: Мнемозина, 2012.

2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. – Гимназия. 2006.

3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. – М.: Просвещение, 1989.

4. Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5–6 класс. – М.: ЗШ МИФИ, 2011.

5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5–6. Пособие для учащихся 6-х классов заочной школы МИФИ. – М.: ЗШ МИФИ, 2011.

6. Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5–6 классов средней школы. – М.: Просвещение, Библиотека учителя математики, 1989.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-сайт «Школьный помощник» (Источник)

2. Интернет-сайт math-prosto.ru (Источник)

3. Интернет-сайт «ЯКласс» (Источник)

Домашнее задание

1. Чему равна длина окружности, если ее радиус равен 31 дм, 200 см, 3200 мм. ()?

2. Окружность арены во всех цирках мира имеет длину 40,8 м. Найдите диаметр и площадь арены.

3. Останкинская телебашня в Москве опирается на площадку, имеющую форму кольца. Диаметр наружной окружности – 63 м, а внутренней – 14 м. Вычислить площадь фундамента башни.

Похожие записи:

Как выучить таблицу умножения Онлайн гадание на таро “позвонит ли он мне” Фитнес-мифы: нельзя есть два часа после тренировки 7 простых рецептов, как очистить электрочайник в домашних условиях Как крепится накладная мойка к тумбе кухни? Старый знакомый любисток снова в моде