Длина окружности

Через какие параметры ее можно найти

Окружность, радиус которой равен r, а центр совпадает с началом декартовой системы координат, можно описать уравнением:

\(r^{2}=x^{2}+y^{2}\)

Данная формула в алгебре является основной.

Если имеется окружность, радиус которой равен r, а центр совпадает с точкой, имеющей координаты (a, b) в декартовой системе координат, то уравнение рассматриваемой окружности приобретает следующий вид:

\(r^{2}=(x-a)^{2}+(y-b)^{2}
\)

Параметрическое уравнение окружности, которая имеет радиус r и центр в точке с координатами (a, b) в декартовой системе координат, записывают следующим образом:

\(\begin{cases}x = a + r cos t\\y = b + r sin t\end{cases}
\)

Вписанные и описанные окружности

Окружность и треугольник

• центр вписанной окружности — точка пересечения
  ,
  ее радиус r вычисляется по формуле:

r = ,

где S — площадь треугольника, а —
полупериметр;

центр описанной окружности — точка пересечения
,
ее радиус Rвычисляется по формуле:

R =
,

R = ;

здесь a, b, c — стороны треугольника,
— угол, лежащий против стороны a, S — площадь треугольника;

центр описанной около окружности лежит на середине ;

центр описанной и вписанной окружностей треугольника совпадают только
в том случае, когда этот треугольник — .

Окружность и четырехугольники

• около
  можно описать окружность тогда и только тогда, когда сумма его внутренних
  противоположных углов равна 180°:

 +
 =  +
 = 180°;

в можно вписать
окружность тогда и только тогда, когда у него равны суммы противоположных
сторон:

a
+ c = b + d;

• около можно
  описать окружность тогда и только тогда, когда он является ;
• около
  можно описать окружность тогда и только тогда, когда эта
  — ; центр
  окружности лежит на пересечении оси симметрии
  с
  к боковой стороне;
• в можно вписать
  окружность тогда и только тогда, когда он является .

Окружность, вписанная в треугольник

Окружность, вписанная в треугольник, соприкасается с каждой стороной этой фигуры лишь в одной точке. В один треугольник возможно вписать лишь одну окружность.

Радиус такой окружности будет зависеть от следующих параметров треугольника:

1. Длин сторон треугольника.
2. Его площади.
3. Его периметра.
4. Величины углов треугольника.

Для того чтобы вычислить радиус вписанной окружности в треугольник, не всегда обязательно знать все перечисленные выше параметры, поскольку они взаимосвязаны между собой через тригонометрические функции.

Вычисление с помощью полупериметра

Чтобы рассчитать величину радиуса вписанной окружности в треугольник, необходимо учитывать следующие параметры:

1. Если известны длины всех сторон геометрической фигуры (обозначим их буквами a, b и c), то вычислять радиус придётся путём извлечения квадратного корня.
2. Приступая к вычислениям, необходимо добавить к исходным данным ещё одну переменную — полупериметр (р). Его можно рассчитать, сложив все длины и полученную сумму разделив на 2. p = (a+b+c)/2. Таким образом можно существенно упростить формулу нахождения радиуса.
3. В целом формула должна включать в себя знак радикала, под который помещается дробь, знаменателем этой дроби будет величина полупериметра р.
4. Числителем данной дроби будет представлять собой произведение разностей (p-a)*(p-b)*(p-c)
5. Таким образом, полный вид формулы будет представлен следующим образом: r = √(p-a)*(p-b)*(p-c)/p).

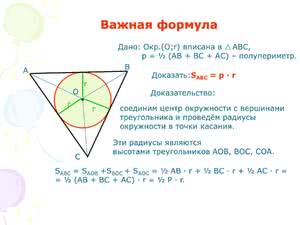
Вычисление с учётом площади треугольника

Если нам известна площадь треугольника и длины всех его сторон, это позволит найти радиус интересующей нас окружности, не прибегая к извлечению корней.

1. Для начала нужно удвоить величину площади.
2. Результат делится на сумму длин всех сторон. Тогда формула будет выглядеть следующим образом: r = 2*S/(a+b+c).
3. Если воспользоваться величиной полупериметра, можно получить совсем простую формулу: r = S/p.

Расчёт с помощью тригонометрических функций

Если в условии задачи присутствует длина одной из сторон, величина противоположного угла и периметр, можно воспользоваться тригонометрической функцией — тангенсом. В этом случае формула расчёта будет иметь следующий вид:

r = (P /2- a)* tg (α/2), где r — искомый радиус, Р — периметр, а — значение длины одной из сторон, α — величина противоположного стороне, а угла.

Радиус окружности, которую необходимо будет вписывать в правильный треугольник, можно найти по формуле r = a*√3/6.

Как использовать эти понятия в жизни

Вообще с этими понятиями знакомы практически все, кто учил геометрию в школе. Взрослые тоже часто сталкиваются с ними, когда помогают детям делать домашнее задание или просто проверяют его.

Также эти понятия очень часто используются в черчении, к примеру, в архитектуре, когда планируется сделать круглое окно, арку или другую круглую деталь.

В ландшафте тоже не обойтись без радиуса и диаметра, ведь именно они позволят поделить круг на несколько частей, создав яркие цветочные композиции

Последние будут не только радовать глаза, но и помогут отвлечь внимание гостей от грядок с овощами

Во время конструирования одежды тоже часто встречаются понятия радиус и диаметр. Например, когда шьют шляпы, юбки или круглые накладные воротники.

Понятия диметр и радиус часто используются в программировании и создании сайтов. К примеру, многие создают программы для коррекции кругов (последние используются в разных сферах).

Важно обратить внимание, что понятия диаметр и радиус касаются не только круга. Круг – это фигура, которая лежит на определенной плоскости. Но в геометрии фигуры не всегда лежат на плоскости, некоторые находятся в пространстве

И понятия круг в пространстве вообще не существует, в нем используются объемные фигуры, например, эллипс, цилиндр, конус или шар. Для вычисления объема всех этих фигур тоже понадобится определять диаметр и радиус

Но в геометрии фигуры не всегда лежат на плоскости, некоторые находятся в пространстве. И понятия круг в пространстве вообще не существует, в нем используются объемные фигуры, например, эллипс, цилиндр, конус или шар. Для вычисления объема всех этих фигур тоже понадобится определять диаметр и радиус.

Основные термины

Касательная

Прямая, имеющая с только одну общую точку, называется касательной
к окружности, а их общая точка называется точкой касания прямой
и окружности.

Свойства касательной

1. Касательная к окружности перпендикулярна к радиусу, проведенному в
   точку касания.

Отрезки касательных к окружности, проведенных из одной точки, равны
и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Хорда

Отрезок, соединяющий две точки окружности, называется ее хордой.
Хорда, проходящая через центр окружности, называется диаметром.

Свойства хорд

1. Диаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые
   ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит
   пополам хорду, то он перпендикулярен этой хорде.

Дуги, заключенные между параллельными хордами, равны.

Если две хорды окружности, AB и CD пересекаются в точке
M, то произведение отрезков одной хорды равно произведению отрезков
другой хорды: AM•MB = CM•MD.

Что такое окружность — определение и свойства

Определение

Окружность является совокупностью множества точек, расположенных на плоскости, и равноудаленных от определенной точки О, которая представляет собой центр окружности.

Определение

Единичной окружностью называют такую окружность, радиус которой равен единице.

Определение

Круг представляет собой часть плоскости, которая ограничена окружностью.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Окружность обладает рядом характерных свойств:

1. Диаметр окружности в два раза больше, чем радиус окружности: D = 2r.
2. Минимальное расстояние от центра окружности к секущей (хорде) в любом случае меньше, чем радиус окружности.
3. Если существуют три точки, расположенные не на одной прямой, то через них можно провести единственно возможную окружность.
4. Из всех замкнутых кривых, обладающих аналогичной длиной, окружность обладает максимально возможной площадью.
5. При соприкосновении пары окружностей в определенной точке, эта точка расположена на прямой, которая проходит через центры заданных окружностей.

Другие понятия

Существует еще несколько понятий, которые могут пригодиться тем, кто работает с диаметром или радиусом:

• Дуга. Это кривая линия, которая является частью окружности. Ее измеряют в градусах. Сумма всех дуг составляет 360 градусов.
• Хорда. В отличие от кривой дуги это прямой отрезок, который соединяет две точки на окружности. Хорда отличается и диаметра – последний всегда равен двум радиусам и всегда проходит через центральную точку круга. Хорда же может быть длиннее или короче радиуса и никогда не проходит через центральную точку на круге.
• Сектор. Простыми словами, круг – это торт или пирог. Сектор же это треугольный кусок, который вырезается из этого пирога или торта.
• Касательная. Это линия, которая проходит рядом с кругом так, что соприкасается только с одной точкой на окружности.

Все перечисленные выше понятия пригодятся не только тем, кто учит геометрию, но и тем, кто имеет дело с кругами в других сферах. В математике существует несколько формул, которые помогут выяснить величину любого из описанных выше понятий по заданным параметрам.

Окружность, вписанная в прямоугольный треугольник

В прямоугольный треугольник можно вписать только одну окружность. Центр такой окружности одновременно служит точкой пересечения всех биссектрис. Эта геометрическая фигура имеет некоторые отличительные черты, которые необходимо учесть, вычисляя радиус вписанной окружности.

1. Для начала необходимо выстроить прямоугольный треугольник с заданными параметрами. Построить такую фигуру можно по размеру её одной стороны и величинам двух углов или же по двум сторонам и углу между этими сторонами. Все эти параметры должны быть указаны в условии задачи. Треугольник обозначается как АВС, причём С — это вершина прямого угла. Катеты при этом обозначаются переменными, а и b, а гипотенуза — переменной с.
2. Для построения классической формулы и вычисления радиуса окружности необходимо найти размеры всех сторон описанной в условии задачи фигуры и по ним вычислить полупериметр. Если в условиях даются размеры двух катетов, по ним можно вычислить величину гипотенузы, исходя из теоремы Пифагора.
3. Если в условии дан размер одного катета и одного угла, необходимо понять, прилежащий этот угол или противолежащий. В первом случае гипотенуза находится с помощью теоремы синусов: с=a/sinСАВ, во втором случае применяют теорему косинусов с=a/cosCBA.
4. Когда все расчёты выполнены и величины всех сторон известны, находят полупериметр по формуле, описанной выше.
5. Зная величину полупериметра, можно найти радиус. Формула представляет собой дробь. Её числителем является произведение разностей полупериметра и каждой из сторон, а знаменателем —величина полупериметра.

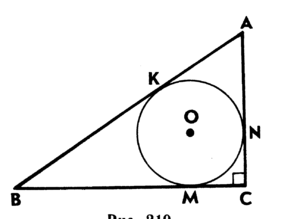
Следует заметить, что числитель данной формулы является показателем площади. В этом случае формула нахождения радиуса гораздо упрощается — достаточно разделить площадь на полупериметр.

Определить площадь геометрической фигуры можно и в том случае, если известны оба катета. По сумме квадратов этих катетов находится гипотенуза, далее вычисляется полупериметр. Вычислить площадь можно, умножив друг на друга величины катетов и разделив полученное на 2.

Если в условиях даны длины и катетов и гипотенузы, определить радиус можно по очень простой формуле: для этого складываются длины катетов, из полученного числа вычитается длина гипотенузы. Результат необходимо разделить пополам.

Углы в окружности

Центральным углом в окружности называется плоский угол с вершиной
в ее центре.

Угол, вершина которого лежит на окружности, а стороны пересекают эту
окружность, называется вписанным углом.

Любые две точки окружности делят ее на две части. Каждая из этих частей
называется дугой окружности. Мерой дуги может служить мера соответствующего
ей центрального угла.

Дуга называется полуокружностью, если отрезок, соединяющий её
концы, является диаметром.

Свойства углов, связанных с окружностью

1. Вписанный угол либо равен половине соответствующего ему центрального
   угла, либо дополняет половину этого угла до 180°.

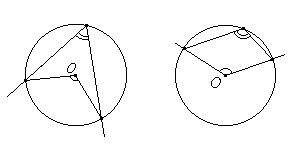
Углы, вписанные в одну окружность и опирающиеся на одну и ту же дугу,
равны.

Вписанный угол, опирающийся на , равен
90°.

Угол, образованный к окружности и
, проведенной через точку касания, равен половине
дуги, заключенной между его сторонами.

Свойства окружности

1. Прямая может не иметь с окружностью общих точек; иметь с окружностью
   одну общую точку (); иметь с ней
   две общие точки (секущая).
2. Через три точки, не лежащие на одной прямой, можно провести окружность,
   и притом только одну.
3. Точка касания двух окружностей лежит на линии, соединяющей их центры.

Теорема о касательной и секущей

Если из точки, лежащей вне окружности, проведены
и , то квадрат длины касательной равен произведению
секущей на ее внешнюю часть: MC2 = MA•MB.

Теорема о секущих

Если из точки, лежащей вне окружности, проведены две ,
то произведение одной секущей на её внешнюю часть равно произведению другой
секущей на её внешнюю часть. MA•MB = MC•MD.

Примеры задач с решением

Задача 1

Существует некая окружность, вписанная в квадрат, радиус которой равен 39. Необходимо рассчитать площадь квадрата, представленного на графике.

Решение

Сначала требуется построить радиусы ОА и ОВ к точке, в которой окружность касается с квадратом.

Отрезок АВ можно определить, как сторону квадрата.

х = АВ = 39 + 39 = 78

Площадь квадрата:

\(S = x^{2} = 78^{2} = 6084\)

Ответ: площадь квадрата составляет 6084.

Задача 2

Диаметр окружности равен 5 см. Необходимо определить, какова длина заданной окружности.

Решение

Длину окружности можно рассчитать по формуле:

\(L = \pi D\)

Исходя из условий задачи, подставим значение диаметра в уравнение и выполним вычисления:

L = 3,14 * 5 = 15,7 (см)

Ответ: длина окружности равна 15,7 см.

Задача 3

Существует окружность с радиусом 3,5 м. Требуется определить длину данной окружности.

Решение

В первую очередь следует определить величину диаметра рассматриваемой окружности:

D = 2r = 3,5 * 2 = 7 (м)

Далее можно рассчитать длину окружности:

\(L = \pi D = 3,14 * 7 = 21,98 (м)\)

Ответ: длина окружности составляет 21,98 м.

Задача 4

Длина окружности составляет 7,85 м. Требуется определить радиус этой окружности.

Решение

Рассчитать радиус окружности, зная ее длину, можно путем деления длины на \(2\pi:\)

\(R = \frac{C}{2\pi}\)

Таким образом:

\(R = \frac{7,85}{2 * 3,14} = \frac{7,85}{6,28} = 1,25 (м)\)

Похожие записи:

Как в майнкрафте сделать щит Как правильно и быстро почистить кальмары от пленки в домашних условиях: пошаговая инструкция (видео) Способы, срок и условия хранение укропа на зиму 7 самых красивых и неприхотливых комнатных папоротников Причины быстрой кристаллизации меда и ее связь с качеством продукта Можжевеловый веник для бани: польза и как пользоваться