Теорема пифагора

Пример задачи №2

Условие: вычислить диагональ, проведенную в прямоугольнике с меньшей стороной, равной 41. Если известно, что она делит угол на такие, которые соотносятся как 2 к 1.

В этой задаче диагональ прямоугольника является наибольшей стороной в треугольнике с углом 90º. Поэтому все сводится к тому, как найти гипотенузу.

В задаче идет речь об углах. Это значит, что нужно будет пользоваться одной из формул, в которых присутствуют тригонометрические функции. А сначала требуется определить величину одного из острых углов.

Пусть меньший из углов, о которых идет речь в условии, будет обозначен α. Тогда прямой угол, который делится диагональю, будет равен 3α. Математическая запись этого выглядит так:

Из этого уравнения просто определить α. Он будет равен 30º. Причем он будет лежать напротив меньшей стороны прямоугольника. Поэтому потребуется формула, описанная в способе №3.

Гипотенуза равна отношению катета к синусу противолежащего угла, то есть:

Доказательства теоремы Пифагора.

На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема

Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие

можно объяснить лишь фундаментальным значением теоремы для геометрии.

Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них:

доказательства методом площадей, аксиоматические и экзотические доказательства (например,

с помощью дифференциальных уравнений).

1. Доказательство теоремы Пифагора через подобные треугольники.

Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся

напрямую из аксиом. В частности, оно не использует понятие площади фигуры.

Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим

её основание через H.

Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC.

Введя обозначения:

получаем:

,

что соответствует –

Сложив a2 и b2, получаем:

или , что и требовалось доказать.

2. Доказательство теоремы Пифагора методом площадей.

Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они

используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.

Доказательство через равнодополняемость.

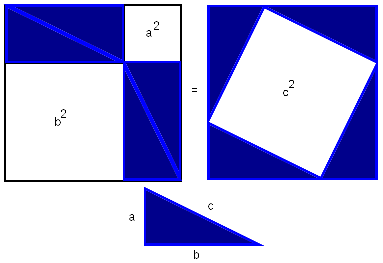Расположим четыре равных прямоугольных

треугольника так, как показано на рисунке

справа.

Четырёхугольник со сторонами c – квадратом,

так как сумма двух острых углов 90°, а

развёрнутый угол — 180°.

Площадь всей фигуры равна, с одной стороны,

площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырёх треугольников и

площади внутреннего квадрата.

Что и требовалось доказать.

3. Доказательство теоремы Пифагора методом бесконечно малых.

​

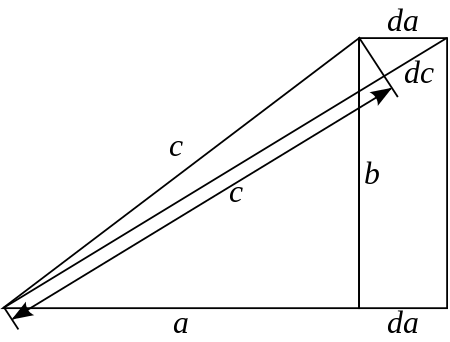
Рассматривая чертёж, показанный на рисунке, и

наблюдая изменение стороны a, мы можем

записать следующее соотношение для бесконечно

малых приращений сторон с и a (используя подобие

треугольников):

Используя метод разделения переменных, находим:

Более общее выражение для изменения гипотенузы в случае приращений обоих катетов:

Интегрируя данное уравнение и используя начальные условия, получаем:

Таким образом, мы приходим к желаемому ответу:

Как нетрудно видеть, квадратичная зависимость в окончательной формуле появляется благодаря линейной

пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми

вкладами от приращения разных катетов.

Более простое доказательство можно получить, если считать, что один из катетов не испытывает приращения

(в данном случае катет b). Тогда для константы интегрирования получим:

Формулировка теоремы

Изначальная (геометрическая) формулировка Пифагора гласила:

Теорема

В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Позднее появился алгебраический вариант:

Теорема

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Оба этих определения эквивалентны. Алгебраическое более элементарно, так как оно не оперирует понятием площади, поэтому теорему в этом виде можно проверить просто – измерив длину гипотенузы и катетов, сделав затем необходимое вычисление.

Способ под номером 3: даны катет и угол, который лежит напротив него

Чтобы не запутаться в формулах, введем обозначение для этого угла — β, а сторону оставим прежнюю «а». В этом случае потребуется другая тригонометрическая функция — синус.

Как и в предыдущем примере, синус равен отношению катета к гипотенузе. Формула этого способа выглядит так:

с = а / sin β.

Для того чтобы не запутаться в тригонометрических функциях, можно запомнить простое мнемоническое привило: если в задаче идет речь о противолежащем угле, то нужно использовать синус, если — о прилежащем, то косинус

Следует обратить внимание на первые гласные в ключевых словах. Они образуют пары о-и или и-о

Историческая справка

Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая
соотношение между сторонами прямоугольного треугольника.

В древнекитайской книге «Чжоу би суань цзин» говорится о пифагоровом треугольнике со сторонами 3, 4 и 5. Крупнейший немецкий
историк математики Мориц Кантор (1829 — 1920) считает, что равенство $3^{2}+4^{2}=5^{2}$ было известно уже египтянам ещё около
2300 г. до н.э. По мнению ученого, строители строили тогда прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте приводится приближённое вычисление гипотенузы равнобедренного
прямоугольного треугольника.

На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является
единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным
значением теоремы для геометрии.

Формула гипотенузы равнобедренного прямоугольного треугольника

1001student.ru > Геометрия > Формула гипотенузы равнобедренного прямоугольного треугольника

В повседневной жизни каждому человеку время от времени приходится решать задачи из школьной программы.

Несмотря на то что многие в детстве считали эти знания ненужными, сейчас все понимают, что были неправы.

Например, в любой момент может понадобиться найти длину гипотенузы равнобедренного треугольника, формулу расчета которой несложно вывести самостоятельно. Для этого следует вспомнить законы геометрии.

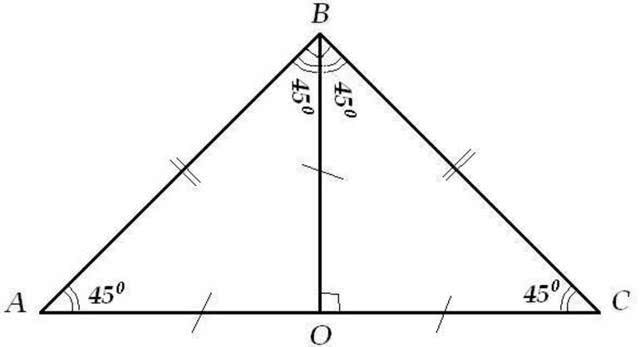
Законы геометрии

В первую очередь надо определиться с терминами. Чтобы в дальнейшем было понятно, что означают те или иные геометрические понятия, необходимо вспомнить следующие определения:

• треугольник;
• сторона;
• угол;
• бедро;
• равнобедренный;
• равносторонний;
• прямоугольный;
• гипотенуза;
• катет;
• теорема.

Треугольник – это замкнутая геометрическая фигура, состоящая из трех точек, соединенных последовательно тремя отрезками, которые являются сторонами этой фигуры. Прямые, исходящие из одной точки, образуют угол.

Каждый треугольник состоит из трех сторон. Исходящие из одной вершины стороны называются бедрами, поэтому фигура, у которой минимум две стороны имеют равную длину, называется равнобедренной. В случае когда все стороны фигуры равны, она называется равносторонним треугольником.

Треугольник, в котором есть прямой угол, называется прямоугольным. Прямым в геометрии называется угол в 90 градусов. Поскольку в каждой треугольной фигуре сумма всех углов равна 180 градусов, то в ней может быть только один прямой угол. Гипотенуза в переводе с греческого языка означает «натянутая» – это сторона треугольника, которая лежит напротив прямого угла.

Катет – это одна из двух других сторон прямоугольного треугольника, тоже греческое слово, которое в переводе означает опущенный, отвесный или перпендикуляр. Катеты одновременно являются бедрами, а в равнобедренном прямоугольном треугольнике гипотенуза служит еще и основанием.

Теорема – это истина, которую надо доказать. Одно из самых известных и значимых правил геометрии – это теорема Пифагора.

Теорема Пифагора

Древнегреческий математик и философ Пифагор, если верить историкам, первым нашел правильный расчет соотношения размеров длин катетов и гипотенузы. Согласно теореме Пифагора, длина гипотенузы в квадрате равна сумме длин катетов, возведенных в квадрат. Можно кратко описать теорему, обозначив гипотенузу буквой Г, а катеты — К1 и К2:

Г2 =К12 + К22

Как вычислить формулу

Если довериться логике и Пифагору, то легко высчитать, что размер самой длинной стороны треугольника будет равен квадратному корню из суммы квадратов двух меньших сторон. Если учесть, что в равнобедренном треугольнике катеты равны, то формулу можно усовершенствовать.

Гипотенузу равнобедренного треугольника можно рассчитать путем вычисления квадратного корня из квадрата длины катета, умноженного на два.

Вопрос на засыпку

Чтобы ответить на вопрос, как найти гипотенузу равностороннего треугольника, надо вспомнить, чему равен каждый его угол.

При любой длине сторон в этой фигуре, сумма всех углов неизменна и равна 180 градусов, соответственно каждый из них в этой фигуре равен 60 градусов.

Прямого угла в такой фигуре не может быть по определению, поэтому нет и гипотенузы. Значит, поставленный вопрос некорректен и не имеет ответа.

Практическое применение

В каких сферах повседневной жизни может понадобиться знание формулы? Эта тема находит практическое применение в архитектуре, строительстве, физике, математике, астрономии и других областях народного хозяйства, например:

Для дизайнера, работающего над планировкой дома или квартиры, важно знать, является ли конкретный угол прямым. Высчитав длину всех сторон, можно сделать вывод о размере угла.
В организациях, занимающихся оптовой торговлей или транспортными услугами, для правильного построения логистической схемы распределения товара между розничными точками порой необходимо рассчитывать самые краткие и оптимальные пути передвижения между различными объектами.
На даче или огороде можно правильно рассчитать длину лестницы, необходимой для установки на определенную высоту под определенным углом, чтобы легко взбираться на мансарду или чердак.. Если внимательно оглядеться вокруг, можно различить большое количество разнообразных геометрических фигур

Если внимательно оглядеться вокруг, можно различить большое количество разнообразных геометрических фигур.

Где геометрия, там и возможности использовать ее правила и формулы расчетов, в том числе и формулу длины гипотенузы.

Свойство медианы прямоугольного треугольника

Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.

Пусть СМ — медиана прямоугольного треугольника АВС с прямым углом С.
Проведем через вершину В прямую m, параллельную катету АС.
Через вершину А проведем прямую n, параллельную катету ВС.

Прямые m и n пересекаются в точке К.

Мы получили прямоугольник АКВС (параллелограмм, в котором угол С – прямой).
Диагонали прямоугольника равны и в точке пересечения делятся пополам.

Задача ЕГЭ по теме «Медиана прямоугольного треугольника»
В треугольнике ABC угол ACB равен , угол B равен , CD — медиана. Найдите угол ACD. Ответ дайте в градусах.

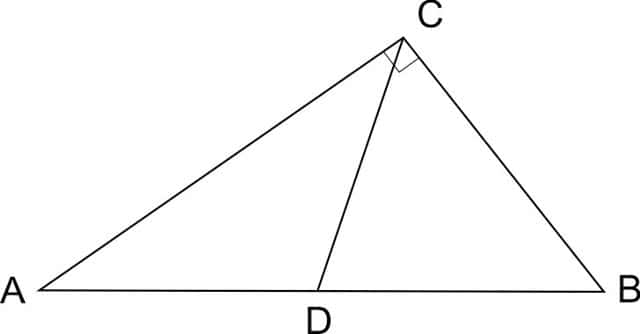
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы. Это значит, что треугольник CBD – равнобедренный, CD = BD. Тогда

Как найти гипотенузу: 4 способа поиска ответа

После изучения темы про прямоугольные треугольники ученики часто выбрасывают из головы всю информацию о них. В том числе и то, как найти гипотенузу, не говоря уже о том, что это такое.

И напрасно. Потому что в дальнейшем диагональ прямоугольника оказывается этой самой гипотенузой, и ее нужно найти. Или диаметр окружности совпадает с самой большой стороной треугольника, один из углов которого прямой. И найти ее без этого знания невозможно.

Существует несколько вариантов того, как найти гипотенузу треугольника. Выбор метода зависит от исходного набора данных в условии задачи величин.

Пример задачи №1

Условие: в прямоугольном треугольнике проведены медианы к обоим катетам. Длина той, которая проведена к большей стороне, равна √52. Другая медиана имеет длину √73. Требуется вычислить гипотенузу.

Так как в треугольнике проведены медианы, то они делят катеты на два равных отрезка. Для удобства рассуждений и поиска того, как найти гипотенузу, нужно ввести несколько обозначений. Пусть обе половинки большего катета будут обозначены буквой «х», а другого — «у».

Теперь нужно рассмотреть два прямоугольных треугольника, гипотенузами у которых являются известные медианы. Для них нужно дважды записать формулу теоремы Пифагора:

(2у) 2 + х 2 = (√52) 2

(у) 2 + (2х) 2 = (√73) 2 .

Эти два уравнения образуют систему с двумя неизвестными. Решив их, легко можно будет найти катеты исходного треугольника и по ним его гипотенузу.

Сначала нужно все возвести во вторую степень. Получается:

Из второго уравнения видно, что у 2 = 73 — 4х 2 . Это выражение нужно подставить в первое и вычислить «х»:

4(73 — 4х 2 ) + х 2 = 52.

292 — 16 х 2 + х 2 = 52 или 15х 2 = 240.

Из последнего выражения х = √16 = 4.

Теперь можно вычислить «у»:

у 2 = 73 — 4(4) 2 = 73 — 64 = 9.

По данным условия получается, что катеты исходного треугольника равны 6 и 8. Значит, можно воспользоваться формулой из первого способа и найти гипотенузу:

√(6 2 + 8 2 ) = √(36 + 64) = √100 = 10.

Ответ: гипотенуза равна 10.

Калькулятор периметра прямоугольного треугольника

Прямоугольный треугольник — простая, но крайне важная для математики фигура. Знание о его свойствах и умение оперировать основными параметрами прямоугольного треугольника позволит вам справиться как со школьными, так и с реальными задачами.

Геометрия прямоугольного треугольника

Геометрически треугольник — это три точки, не лежащие на одной прямой, которые соединены между собой отрезками. Прямоугольный треугольник — фигура, две стороны которой образуют прямой угол.

Эти стороны называются катетами треугольника, а третья, самая длинная сторона, носит название гипотенузы.

Соотношение квадратов катетов и гипотенузы устанавливает теорема Пифагора — одна из фундаментальных теорем евклидовой геометрии.

Соотношения гипотенузы и катетов также положили основу для целого раздела математики — тригонометрии.

Изначально синусы и косинусы определялись как функции углов прямоугольного треугольника, но в современном значении тригонометрические функции расширены на всю числовую ось.

Сегодня тригонометрия используется во многих областях человеческой деятельности: от астрономии и океанографии до анализа финансовых рынков и разработки компьютерных игр.

Прямоугольный треугольник в реальности

Непосредственно прямоугольный треугольник встречается в реальности на каждом углу, как в прямом, так и в переносном смысле.

Форму прямоугольного треугольника имеют грани тетраэдров и призм, которые в реальности превращаются в детали машин, керамическую плитку или скаты крыш.

Угольник — чертежный инструмент, с которым человек впервые встречается на уроке геометрии, имеет форму именно прямоугольного треугольника и используется в проектировании, строительстве и столярном деле.

Периметр треугольника

Периметр — это численная оценка длин всех сторон плоской геометрической фигуры. Периметр n-угольника находится как сумма длин n сторон. Для определения периметра прямоугольного треугольника используется простая формула:

• P = a + b + c,
• a и b – катеты, c – гипотенуза.
• Вычисляя периметр треугольника вручную, вам пришлось бы измерять все три стороны, проводить дополнительные тригонометрические операции или вычисления по теореме Пифагора. Используя онлайн-калькулятор вам достаточно узнать следующие пары переменных:

• два катета;
• катет и угол;
• гипотенуза и угол.

В школьных задачах или на практике вам будут заданы исходные данные, поэтому калькулятор позволяет найти периметр, зная разные пары параметров. Кроме того, инструмент автоматически рассчитывает все остальные атрибуты прямоугольного треугольника, то есть длины всех сторон и величины всех углов. Рассмотрим пару примеров.

Школьная задача

Пусть в школьной задаче вам задан прямоугольный треугольник с длиной катета равным 5 см и прилежащим углом, величина которого составляет 60 градусов. Требуется найти периметр геометрической фигуры.

Онлайн-калькулятор сопровождается рисунком, на котором изображены стороны и углы прямоугольного треугольника. Мы видим, что если катет a = 5 см, то его прилежащий угол — это угол бета.

Это важный момент, так как если вы используете для расчетов угол альфа, то результат будет неверным. Вбиваем эти данные в форму и получаем ответ в виде:

Помимо непосредственно периметра, наша программа также определила величину противолежащего угла, а также длину второго катета и гипотенузы.

Обустройство клумбы

Допустим, вы хотите сделать ограду для клумбы, которая имеет форму прямоугольного треугольника. Для этого вам необходимо узнать периметр фигуры. Конечно, в реальности вы можете просто замерить все три стороны, но легко упростить себе задачу и измерить только два катета. Пусть они имеют длину 8 и 15 метров. Вбиваем эти данные в форму калькулятора и получаем ответ:

P = 40

Итак, вам понадобится закупить материалы для обустройства 40 метров ограды. Наш калькулятор также подсчитал длину гипотенузы — 17 метров. Числа 8, 15 и 17 составляют пифагорову тройку — натуральные числа, которые удовлетворяют условиям теоремы Пифагора.

Заключение

Прямоугольные треугольники получили широкое распространение в повседневности, поэтому определение площади или периметра геометрической фигуры наверняка пригодится вам при решении школьных задач или бытовых вопросов.

Теорема Пифагора — краткая история

Соотношение между сторонами прямоугольного треугольника в том или ином виде было известно многим древним цивилизациям (египетской, шумерской и др.), но первая известная формулировка принадлежит греческому философу и математику Пифагору в V в. до н.э. Об этом известно из труда «Начала», который написал Евклид приблизительно в 300 г. до н. э.

Теорема Пифагора используется для доказательства многих других теорем геометрии. Математиками разработано несколько обобщений, например, для произвольных треугольников, для многомерных пространств. При этом, теорема Пифагора выполняется только в евклидовых геометриях, в иных случаях она не действует.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

• для гипотенузы (с):
  • длины катетов a и b
  • длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
  • длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
• для катета:
  • длину гипотенузы (с) и длину одного из катетов
  • длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
  • длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
  • длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
  • длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)

Введите их в соответствующие поля и получите результат.

Найти гипотенузу (c)

Найти гипотенузу по двум катетам

Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?

следовательно: c = √ a² + b²

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:

c = √ 3² + 4² = √ 9 + 16 = √ 25 = 5 см

Найти гипотенузу по катету и прилежащему к нему острому углу

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:

c = 2 / cos(60) = 2 / 0.5 = 4 см

Найти гипотенузу по катету и противолежащему к нему острому углу

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:

c = 2 / sin(30) = 2 / 0.5 = 4 см

Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.

Найти катет

Найти катет по гипотенузе и катету

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:

a = √ 5² — 4² = √ 25 — 16 = √ 9 = 3 см

Найти катет по гипотенузе и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:

b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см

Найти катет по гипотенузе и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:

a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см

Найти катет по второму катету и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:

b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см

Найти катет по второму катету и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:

http://razuznai.ru/kak_najti_katety_esli_izvestna_gipotenuza.htmlhttp://www.syl.ru/article/182058/mod_kak-nayti-gipotenuzu-sposoba-poiska-otvetahttp://poschitat.online/storony-pryamougolnogo-treugolnika

Как найти равные катеты, при известной гипотенузе

• гипотенуза (обозначим ее буквой «c») равна х см: c=x;
• первый катет (обозначим его буквой «a») равен второму катету ((обозначим его буквой «b»): a=b;

В этом варианте решение задачи основывается на использовании теоремы Пифагора. Ее применяют к прямоугольным треугольникам и основной ее вариант звучит, как: «Квадрат гипотенузы равен сумме квадратов катетов». Так, как катеты у нас равны, то мы можем обозначать оба катета одним и тем же сиволом: a=b, значит — a=a.

1. Подставляем наши условные обозначения в теорему (с учетом вышеизложенного): c^2=a^2+a^2,
2. Далее максимально упрощаем формулу: с^2=2*(a^2) — группируем, с=√2*а — подносим обе части уравнения к квадратному кореню, a=c/√2 — выносим искомое.
3. Подставлем данное значение гипотенузы и получаем решение: a=x/√2

Как найти гипотенузу через угол?

Еще одним способом, который поможет узнать, чему равна гипотенуза в прямоугольном треугольнике, является вычисление через заданный угол. Для этого нам потребуется вывести величину через формулу синуса. Допустим, нам известна величина катета (А) и значение противолежащего угла (α). Тогда все решение заключается в одной формуле: С=А/sin(α).

Например, если длина катета 40 см, а угол составляет 45°, тогда длину гипотенузы можно вывести следующим образом:

40/sin(45°) = 40/0,71 = 56,33.

Определить искомую величину можно также через косинус заданного угла. Допустим, нам известно значение одного катета (В) и острого прилежащего угла (α). Тогда для решения задачи понадобится одна формула: С=В/ cos(α).

К примеру, если длина катета имеет значение 50 см, а угол составляет 45°, тогда гипотенузу можно вычислить следующим образом:

50/cos(45°) = 50/0,71 = 80,42.

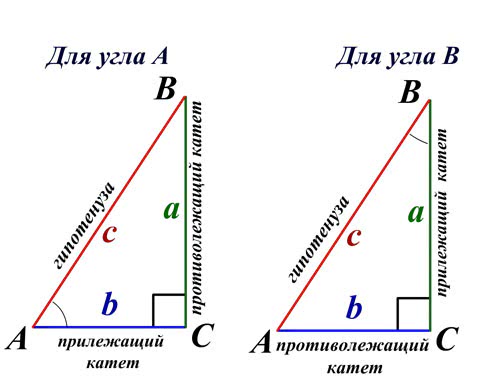
Таким образом, мы рассмотрели основные способы как узнать гипотенузу в треугольнике

В ходе решения задания важно сконцентрировать внимание на имеющихся данных, тогда найти неизвестную величину будет достаточно просто. Необходимо знать всего пару формул и процесс решения задач станет простым и приятным

Вычисление расстояния между двумя точками на координатной плоскости

1. 1

   Выберите две точки на координатной плоскости.

   Чтобы найти расстояние между двумя точками, вы будете рассматривать точки в качестве вершин треугольника, не прилежащих к прямому углу прямоугольного треугольника. Таким образом, вы сможете легко найти катеты треугольника, а затем вычислить гипотенузу, которая равна расстоянию между двумя точками.

   По теореме Пифагора можно вычислить длину отрезка, соединяющего две точки на координатной прямой. Для этого необходимо знать координаты (х,у) каждой точки.

2. 2

   Нанесите точки на координатную плоскость. Отложите координаты (х,у), где координата «х» откладывается по горизонтальной оси, а «у» — по вертикальной. Вы можете найти расстояние между точками без построения графика, но график позволяет визуально представить процесс ваших вычислений.

3. 3

   Найдите катеты треугольника. Вы можете сделать это, измерив длину катетов непосредственно на графике или с помощью формул: |x₁ – x₂| для вычисления длины горизонтального катета, и |y₁ – y₂| для вычисления длины вертикального катета, где (x₁,y₁) – координаты первой точки, а (x₂,y₂) – координаты второй точки.

   • Пример: даны точки: А(6,1) и В(3,5). Длина горизонтального катета:
     • |x₁ – x₂|
     • |3 – 6|
     • | -3 | = 3
   • Длины вертикального катета:
     • |y₁ – y₂|
     • |1 – 5|
     • | -4 | = 4
   • Таким образом, в прямоугольном треугольнике а = 3 и b = 4.

4. 4

   Используйте теорему Пифагора для нахождения гипотенузы. Расстояние между двумя точками равно гипотенузе треугольника, две стороны которого вы только что нашли. Используйте теорему Пифагора, чтобы найти гипотенузу, подставив в формулу найденные значения катетов (a и b).

   • В нашем примере а = 3 и b = 4. Гипотенуза вычисляется следующим образом:

История теоремы

Однако название получено в честь учёного только по той причине, что он первый и, даже единственный человек, который смог доказать теорему.

Немецкий историк математики Кантор утверждал, что о теореме было известно ещё египтянами приблизительно в 2300 году до н. э. Он считал, раньше строили прямые углы благодаря прямоугольным треугольникам со сторонами 3, 4 и 5.

Известный учёный Кеплер говорил, что у геометрии есть незаменимое сокровище – это теорема Пифагора, благодаря которой можно вывести большинство теорем в геометрии.

Раньше теорему Пифагора называли “теоремой невесты” или “теоремой нимфы”. А всё дело в том, что её чертёж был очень похож на бабочку или нимфу. Арабы же, когда переводили текст теоремы, решили, что нимфа означает невеста. Так и появилось интересное название у теоремы.

Способ под номером 4: по радиусу описанной окружности

Теперь, для того чтобы узнать, как найти гипотенузу, потребуется вспомнить свойство окружности, которая описана около прямоугольного треугольника. Оно гласит следующее. Центр окружности совпадает с серединой гипотенузы. Если сказать по-другому, то самая большая сторона прямоугольного треугольника равна диагонали окружности. То есть удвоенному радиусу. Формула для этой задачи будет выглядеть так:

с = 2 * r, где буквой r обозначен известный радиус.

Это все возможные способы того, как находить гипотенузу прямоугольного треугольника. Пользоваться в каждой конкретной задаче нужно тем методом, который больше подходит по набору данных.

Как найти катеты, при известной гипотенузе и угле

• гипотенуза (обозначим ее буквой «c») равна х см: c=x;
• угол β равный q: β=q;

Для решения этой задачи необходимо использовать тригонометрические функции. Найболее популярны две из них:

• функция синуса — синус искомого угла равен отношению противолежащего катета к гипотенузе;
• функция косинуса — косинус искомого угла равен отношению прилежащего катета к гипотенузе;

Вы можете использовать любую. Я наведу пример с использованием первой. Пусть катеты у нас обозначаються символами «a» (прилежащий к углу) и «b» (противолежащий к углу). Соответственно наш угол лежит между катетом «a» и гипотенузой.

1. Подставляем выбранные условные обозначения в формулу:sinβ = b/c
2. Выводим катет:b=c*sinβ
3. Подставляем наши данный и имеем один катет.b=c*sinq

Второй катет можно найти воспользовавшись второй тригонометрической функцией, или же перейти к третьему варианту.

Как найти катеты, при известной гипотенузе и угле

• гипотенуза (обозначим ее буквой «c») равна х см: c=x;
• угол β равный q: β=q;

размер катетов;

Для решения этой задачи необходимо использовать тригонометрические функции. Найболее популярны две из них:

• функция синуса — синус искомого угла равен отношению противолежащего катета к гипотенузе;
• функция косинуса — косинус искомого угла равен отношению прилежащего катета к гипотенузе;

Вы можете использовать любую. Я наведу пример с использованием первой. Пусть катеты у нас обозначаються символами «a» (прилежащий к углу) и «b» (противолежащий к углу). Соответственно наш угол лежит между катетом «a» и гипотенузой.

1. Подставляем выбранные условные обозначения в формулу:sinβ = b/c
2. Выводим катет:b=c*sinβ
3. Подставляем наши данный и имеем один катет.b=c*sinq

Второй катет можно найти воспользовавшись второй тригонометрической функцией, или же перейти к третьему варианту.

Как найти один катет, если известна гипотенуза и другой катет

• гипотенуза (обозначим ее буквой «c») равна х см: c=x;
• катет (обозначим его буквой «b») равен y см: b=y;

размер другого катета (обозначим его буквой «a»);

В этом варианте решением задачи, как и в первом, является использование теоремы Пифагора.

1. Подставляем наши условные обозначения в теорему: c^2=a^2+b^2,
2. Выносим необходимый катет: a^2=c^2-b^2
3. Подносим обе части уравнения к квадратному кореню: a=√(c^2-b^2)
4. Подставляем данные значения и имеем решение: a=√(x^2-y^2)

В жизни нам часто придется сталкиваться с математическими задачами: в школе, в университете, а затем помогая своему ребенку с выполнением домашнего задания. Люди определенных профессий будут сталкиваться с математикой ежедневно. Поэтому полезно запоминать или вспоминать математические правила. В этой статье мы разберем одно из них: нахождение катета прямоугольного треугольника.

Похожие записи:

Как убрать, добавить, занести телефон в черный список Что можно сделать из старых джинсов, идеи и мастер-классы Лёгкие способы оттереть ручку с изделий из кожзама Как помыть стеклянную посуду чтобы блестела? Чесночное масло: польза и вред, приготовление, как принимать? Плита электрическая, что это?