Равнобедренный треугольник. онлайн калькулятор

Формула медианы

Формула медианы в статистике для дискретных данных чем-то напоминает формулу моды. А именно тем, что формулы как таковой нет. Медианное значение выбирают из имеющихся данных и только, если это невозможно, проводят несложный расчет.

Первым делом данные ранжируют (сортируют по убыванию). Далее есть два варианта. Если количество значений нечетно, то медиана будет соответствовать центральному значению ряда, номер которого можно определить по формуле:

где

№_Me – номер значения, соответствующего медиане,

N – количество значений в совокупности данных.

Тогда медиана обозначается, как

Это первый вариант, когда в данных есть одно центральное значение. Второй вариант наступает тогда, когда количество данных четно, то есть вместо одного есть два центральных значения. Выход прост: берется средняя арифметическая из двух центральных значений:

В интервальных данных выбрать конкретное значение не представляется возможным. Медиану рассчитывают по определенному правилу. 

Для начала (после ранжирования данных) находят медианный интервал. Это такой интервал, через который проходит искомое медианное значение. Определяется с помощью накопленной доли ранжированных интервалов. Где накопленная доля впервые перевалила через 50% всех значений, там и медианный интервал.

Не знаю, кто придумал формулу медианы, но исходили явно из того предположения, что распределение данных внутри медианного интервала равномерное (т.е. 30% ширины интервала – это 30% значений, 80% ширины – 80% значений и т.д.). Отсюда, зная количество значений от начала медианного интервала до 50% всех значений совокупности (разница между половиной количества всех значений и накопленной частотой предмедианного интервала), можно найти, какую долю они занимают во всем медианном интервале. Вот эта доля аккурат переносится на ширину медианного интервала, указывая на конкретное значение, именуемое впоследствии медианой.

Обратимся к наглядной схеме.

Немного громоздко получилось, но теперь, надеюсь, все наглядно и понятно. Чтобы при расчете каждый раз не рисовать такой график, можно воспользоваться готовой формулой. Формула медианы имеет следующий вид:

где x_Me — нижняя граница медианного интервала;

i_Me — ширина медианного интервала;

∑f/2 — количество всех значений, деленное на 2 (два);

S_(Me-1)— суммарное количество наблюдений, которое было накоплено до начала медианного интервала, т.е. накопленная частота предмедианного интервала;

f_Me — число наблюдений в медианном интервале.

Как нетрудно заметить, формула медианы состоит из двух слагаемых: 1 – значение начала медианного интервала и 2 – та самая часть, которая пропорциональна недостающей накопленной доли до 50%. 

Для примера рассчитаем медиану по следующим данным.

Требуется найти медианную цену, то есть ту цену, дешевле и дороже которой по половине количества товаров. Для начала произведем вспомогательные расчеты накопленной частоты, накопленной доли, общего количества товаров.

По последней колонке «Накопленная доля» определяем медианный интервал – 300-400 руб (накопленная доля впервые более 50%). Ширина интервала – 100 руб. Теперь остается подставить данные в приведенную выше формулу и рассчитать медиану.

То есть у одной половины товаров цена ниже, чем 350 руб., у другой половины – выше. Все просто. Средняя арифметическая, рассчитанная по этим же данным, равна 355 руб. Отличие не значительное, но оно есть.

Треугольник

Рис. 1. Треугольник (общий случай)

Итак, треугольник, у которого все стороны имеют разную длину и ни один из углов не равен , называется произвольным (рис. 1).

• В случае, если у треугольника равны две стороны, данный треугольник называется равнобедренным.
• В случае, если у треугольника все стороны одинаковы, он называется равносторонним.
• В случае, если у треугольника один и углов прямой (), он называется прямоугольным.
• Для произвольного треугольника вводят ряд отрезков, характеризующих треугольник и обладающих собственными свойствами:

Для разных типов треугольников поиск длин параметров треугольника может происходить по-разному. Для физических задач использование конкретной формулы диктуется конкретными данными задачи.

Рис. 2. Треугольник (биссектриса)

Биссектриса угла — геометрическое место точек, равноудалённых от сторон этого угла. Т.е. биссектриса — это линия, которая делит угол треугольника пополам (рис. 2). Известно, что биссектриса внутреннего угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.

Для нахождения биссектрисы угла через различные данные можно пользоваться следующими соотношениями:

через две стороны и угол:

Медиана треугольника — отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Все медианы треугольника пересекаются в одной точке: данная точка делит медианы в соотношении 2 к 1, считая от вершины (рис. 3).

Рис. 3. Треугольник (медиана)

Для нахождения медианы треугольника через различные данные можно пользоваться следующими соотношениями:

через две стороны и угол между ними:

Рис. 4. Треугольник (высота)

Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противоположную сторону или на её продолжение (рис. 4).

 Для нахождения высоты треугольника через различные данные можно пользоваться следующими соотношениями:

(5)

через сторону и площадь треугольника ()

(6)

Важно: то, какую формулу выбрать для решения конкретной задачи, зависит от того, что легче найти, исходя из дано

Медианы треугольника

Медиана треугольника — это отрезок, который соединяет вершину треугольника с серединой противоположной стороны. На Рис.1 АМ — медиана треугольника АВС (соединяет вершину А с серединой стороны ВС точкой М, т.е. ВМ = МС).

Любой треугольник имеет три медианы. На Рис.2, АМ, ВК, СD  — медианы треугольника АВС.

Медиана АМ соединяет вершину А с серединой стороны ВС — точкой М (ВМ = МС), медиана ВК соединяет вершину В с серединой стороны АС — точкой К (ВК = КС), медиана СD соединяет вершину С с серединой стороны АВ — точкой D (АD = DB).

Замечательное свойство медиан треугольника: в любом треугольнике медианы пересекаются в одной точке. На Рис.2 медианы АВС пересекаются в точке О. При этом, точка О делит каждую медиану в отношении 2 : 1, считая от вершины, т.е. АО : ОМ = ВО : ОК = СО : DO = 2 : 1.

Советуем посмотреть:

• Треугольник
• Равенство треугольников
• Первый признак равенства треугольников
• Перпендикуляр к прямой
• Биссектрисы треугольника
• Высоты треугольника
• Равнобедренный треугольник
• Свойства равнобедренного треугольника
• Второй признак равенства треугольников
• Третий признак равенства треугольников
• Окружность
• Построения циркулем и линейкой
• Треугольники

Правило встречается в следующих упражнениях:

1. 7 класс
2. Задание 114, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
3. Задание 119, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
4. Задание 158, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
5. Задание 336, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
6. Задание 342, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
7. Задание 440, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
8. Задание 727, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
9. Задание 947, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
10. Задание 1054, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
11. Задание 1281, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

• budu5.com, 2020
• Пользовательское соглашение
• Copyright
• Нашли ошибку?
• Связаться с нами

Треугольник как основа стереометрии

Помимо этого, в 10 и 11 классах в учебную программу добавляется так называемая стереометрия. Данный раздел геометрии отвечает за различные предметы в трехмерном пространстве. Если в классической планиметрии основой для всего является точка, то в стереометрии на первый план выходит ребро. Именно с его помощью и происходит построение большинства геометрических объектов в стереометрии. Но есть 1 тема, которая объединяет 2 разные раздела геометрии — треугольник и все, что с ним связано. Большинство объектов в стереометрии состоят из множества небольших плоскостей с тремя или четырьмя углами, которые и являются основным объектом построения на ряду с ребром. Соответственно — для нахождения площади объемных шестиугольников, в первую очередь, необходимо знать все необходимые формулы и термины. Так, всего из одной вершины этой сложной геометрической фигуры можно прочертить сразу 4 различных прямых:

• Биссектрису;
• Перпендикуляр;
• Высоту;
• Медиану.

И если первая — просто делит угол пополам, а срединный перпендикуляр и высота зачастую являются одним понятием, медиана имеет множество своих индивидуальных и необычных признаков.

Примеры решения задач

Нет ничего приятнее, чем поупражняться и поискать градусы и длины в равнобедренном треугольнике. Ну… почти ничего.

Задачка раз. Дан ABC: ∠C = 80∘, AB = BC. Найдите ∠B.

Поскольку вы уже знакомы с пятью теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны.
∠A = ∠C = 80∘.
Не должно вас удивить и то, что сумма углов треугольника равна 180∘
∠B = 180∘ − 80∘ − 80∘ = 20∘.
∠B = 20∘

Задачка два. В равнобедренном треугольнике один из углов равен 110∘. Найдите наибольший из внешних углов этого треугольника.

Вспоминаем первую теорему о равенстве углов при основании (а лучше не забываем вовсе). Поскольку сумма углов = 180∘, то второго угла в 110∘ в нём быть не может. Соответственно, известный угол в 110∘ — это угол при вершине. (180∘−110∘)/2=35∘. Внешние углы треугольника равны: 180∘−110∘=70∘,180∘−35∘=145∘,180∘−35∘=145∘. Больший внешний угол равен 145∘

Признаки равнобедренного треугольника

Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.

1. Если у треугольника два угла равны, то этот треугольник — равнобедренный.
2. Если высота треугольника совпадает с его медианой, то такой треугольник — равнобедренный.
3. Если высота треугольника совпадает с его биссектрисой, то такой треугольник — равнобедренный.
4. Если биссектриса треугольника совпадает с его медианой, то такой треугольник снова равнобедренный!
5. Если два угла треугольника равны, такой треугольник является равнобедренным.

Точка пересечения медиан треугольника

Из курса геометрии известно определение медианы треугольника. 

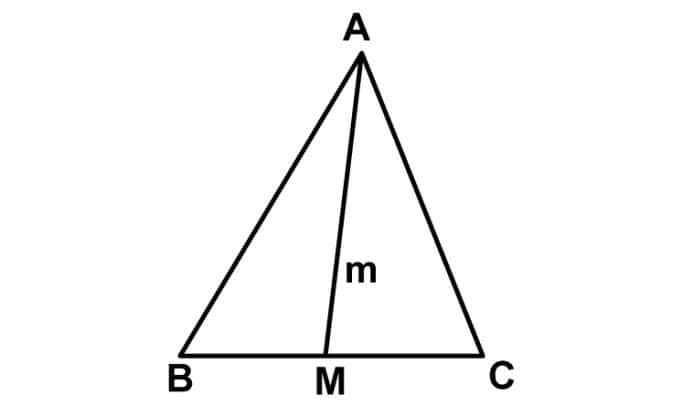
На данном рисунке она обозначена прямой m, которая исходит из вершины А и заканчивается точкой М, являющейся центром стороны ВС.

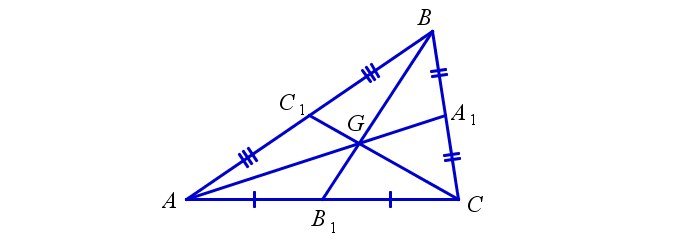
Теперь сделаем чертёж треугольника, на котором укажем замечательную точку пересечения медиан. 

Порядок построения:

1. Для начала постройте абсолютно любой треугольник и обозначьте его буквами А, В и С.

2. На отрезке АВ отметьте центр С₁, на стороне ВС центр А₁, на АС центр В_1.

3. Проведите 3 медианы из вершин. Из угла А – медиана АА₁,из угла В — медиана ВВ₁, из угла С — медиана СС_1.

4. Должно получиться так, как показано на рисунке: три проведённые линии пересекаются в одной точке G (что является их свойством).

Изучим следующее свойство точки пересечения трёх медиан треугольника.

Отрезки медианы треугольника, разделённой замечательной точкой, относятся друг к другу как 2:1. Проследим это свойство на примере используемого нами рисунка:

A₁G = 2AG, B₁G = 2BG, C₁G = 2CG.

Свойства равнобедренного треугольника:

1. В равнобедренном треугольнике углы при основании равны.

Рис. 2. Равнобедренный треугольник

∠ BАC = ∠ BСA

2. Биссектрисы, медианы и высоты, проведённые из этих углов равны между собой.

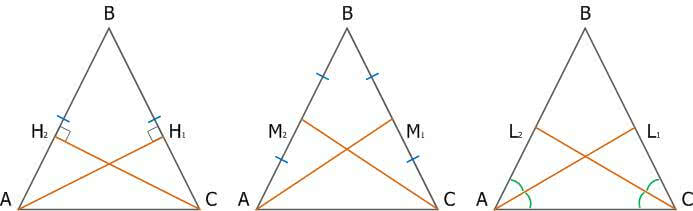
Рис. 3. Равнобедренный треугольник

АН₁ = СН₂ – высота, АМ₁ = СМ₂ – медиана, АL₁ = СL₂ – биссектриса, проведённые из  углов при основании

3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

Рис. 4. Равнобедренный треугольник

ВD – биссектриса, высота и медиана, проведенные к основанию – это один и тот же отрезок

4. Центры вписанной и описанной окружностей лежат на медиане (биссектрисе, высоте), проведенной к основанию равнобедренного треугольника.

Рис. 5. Равнобедренный треугольник

R – радиус описанной окружности, r – радиус вписанной окружности

Свойства

Медиана, независимо от типа треугольника, имеет 5 характерных черт:

1. Если нарисовать из каждой вершины по одной прямой, то можно найти центр тяжести. Именно место пересечения всех 3 лучей и будет точкой равновесия.
2. Также, переплетаясь, они рассекают объект на 6 одинаковых по площади сегментов.
3. Исходя из этого, можно сделать вывод, что 1 луч рассекает треугольник на 2 куска с равной площадью. В случае равнобедренных треугольников и с равными сторонами получившиеся сегменты даже являются симметричными.
4. Самой большей стороне соответствует самая маленькая прямая. В случае равносторонней фигуры, соответственно, все 3 будут иметь одну и ту же длину.
5. Соединяясь, лучи делят друг друга в соотношении 1 к 2.

Медиана в прямоугольном треугольнике

Почему??? При чём тут прямой угол?

Давай смотреть внимательно. Только не на треугольник, а на … прямоугольник.

Ты заметил, что наш треугольник \( \displaystyle ABC\) – ровно половина этого прямоугольника?

Проведём диагональ \( \displaystyle BD\):

Помнишь ли ты, что диагонали прямоугольника равны и делятся точкой пересечения пополам?

Если не помнишь, загляни в тему «Параллелограмм, прямоугольник, ромб…»

Но одна из диагоналей – \( \displaystyle AC\) – наша гипотенуза! Значит, точка пересечения диагоналей – середина гипотенузы \( \displaystyle \Delta ABC\).

Она называлась у нас \( \displaystyle M\).

Значит, половина второй диагонали – наша медиана \( \displaystyle BM\). Диагонали равны, их половинки, конечно же, тоже. Вот и получим \( \displaystyle BM=MA=MC\)

Более того, так бывает только в прямоугольном треугольнике!

Доказывать это утверждение мы не будем, а чтобы в него поверить, подумай сам: разве бывает какой-нибудь другой параллелограмм с равными диагоналями, кроме прямоугольника?

Определение равнобедренного треугольника

Определение 1 (Евклид). Треугольник, в котором длины двух сторон равны между собой называется равнобедренным треугольником.

Равные стороны равнобедренного трекугольника называются боковыми сторонами. Третья сторона равнобедренного треугольника называется основанием треугольника (Рис.1).

Угол между боковыми сторонами равнобедненного треугольника (\( \small \angle A \) ) называется вершинным углом. Углы между основанием и боковыми сторонами (\( \small \angle B, \ \angle C \) ) называются углами при основании.

Существует более общее определение равнобедненого треугольника:

Определение 2 (Современная трактовка). Треугольник, в котором длины хотя бы двух сторон равны между собой называется равнобедренным треугольником.

Из определения 2 следует, что равносторонний треугольник является частным случаем равнобедренного треугольника. Действительно, в качестве равных сторон можно взять любые две стороны равностороннего треугольника, а третья сторона будет основанием.

Теорема о трех медианах треугольника

Что бы это такое значило? Посмотри на рисунок. На самом деле утверждений в этой теореме целых два. Ты это заметил?

Давай попробуем разгадать секрет этой теоремы, то есть доказать ее.

Доказательство теоремы о трех медианах треугольника

Сначала проведем не все три, а только две медианы. Они-то уж точно пересекутся, правда? Обозначим точку их пресечения буквой \( \displaystyle E\).

Соединим точки \( \displaystyle N\) и \( \displaystyle K\). Что получилось?

Конечно, \( \displaystyle NK\) – средняя линяя \( \displaystyle \triangle ABC\). Ты помнишь, что это значит?

• \( \displaystyle NK\) параллельна \( \displaystyle AC\);
• \( \displaystyle NK=\frac{AC}{2}\).

А теперь проведем ещё одну среднюю линию: отметим середину \( \displaystyle AE\) – поставим точку \( \displaystyle F\), отметим середину \( \displaystyle EC\) — поставим точку \( \displaystyle G\).

Теперь \( \displaystyle FG\) – средняя линия \( \displaystyle \triangle AEC\). То есть:

• \( \displaystyle FG\) параллельна \( \displaystyle AC\);
• \( \displaystyle FG=\frac{AC}{2}\).

Заметил совпадения? И \( \displaystyle NK\) , и \( \displaystyle FG\) – параллельны \( \displaystyle AC\). И \( \displaystyle NK=\frac{AC}{2}\), и \( \displaystyle FG=\frac{AC}{2}\).

Что из этого следует?

• \( \displaystyle NK\) параллельна \( \displaystyle FG\);
• \( \displaystyle NK=FG\)

Посмотри теперь на четырехугольник \( \displaystyle NKGF\). У какого четырехугольника противоположные стороны (\( \displaystyle NK\) и \( \displaystyle FG\)) параллельны и равны?

Конечно же, только у параллелограмма!

Значит, \( \displaystyle NKGF\) – параллелограмм. Ну и что?

А давай вспомним свойства параллелограмма. Например, что тебе известно про диагонали параллелограмма? Правильно, они делятся точкой пересечения пополам.

Снова смотрим на рисунок.

Признаки равнобедренного треугольника

Признак 1. Если в треугольнике две стороны равны, то треугольник является равнобедренным.

Признак 1 следует из определения 1.

Признак 2. Если в треугольнике два угла равны, то треугольник является равнобедренным.

Доказательство признака 2 смотрите в статье Соотношения между сторонами и углами треугольника (Следствие 2. Признак равнобедренного треугольника).

Признак 3. Если в треугольнике высота проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.

Доказательство. Пусть в треугольнике \( \small ABC \) \( \small AH \) является высотой и медианой (Рис.4). Тогда \( \small \angle 3=\angle4=90°, \) \( \small CH=HB. \) Треугольники \( \small AHC \) и \( \small AHB \) равны по двум сторонам и углу между ними (): \( \small AH \) − общая сторона, \( \small CH=HB, \) \( \small \angle 3=\angle4. \) Следовательно \( \small AB=AC. \)

Признак 4. Если в треугольнике высота проведенная к одной стороне совпадает с биссектрисой проведенной к этой же стороне, то треугольник является равнобедренным.

Доказательство. Пусть в треугольнике \( \small ABC \) \( \small AH \) является высотой и биссектрисой (Рис.4). Тогда \( \small \angle 3=\angle4=90°, \) \( \small \angle 1=\angle2. \) Треугольники \( \small AHC \) и \( \small AHB \) равны по стороне и прилежащим двум углам (): \( \small AH \) − общая сторона, \( \small \angle 1=\angle 2, \) \( \small \angle 3=\angle4. \) Следовательно \( \small AB=AC. \)

Признак 5. Если в треугольнике биссектриса проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.

Доказательство (Вариант 1). Пусть в треугольнике \( \small ABC \) \( \small AH \) является биссектрисой и медианой (Рис.5). Тогда

Применим теорему синусов для треугольника \( \small AHC \):

Применим теорему синусов для треугольника \( \small AHB \):

тогда, из (5), (6), (7) получим:

Следовательно \( \small \sin \angle C= \sin \angle B. \) Поскольку сумма всех углов треугольника равна 180°, то нам интересует синус углов от 0 до 180°. Учитывая это получим, что синусы углов равны в двух случаях: 1) \( \small \angle C= \angle B, \) 2) \( \small \angle C= 180° — \angle B. \) Поскольку сумма двух углов треугольника меньше 180°: \( \small \angle C + \angle B< 180° \) второй вариант исключается. Т.е. \( \small \angle C= \angle B \) и по признаку 2 треугольник является равнобедренным.

Доказательство (Вариант 2). Пусть в треугольнике \( \small ABC \) \( \small AH \) является биссектрисой и медианой, т.е. \( \small \angle 1=\angle 2, \) \( \small CH=HB \) (Рис.6). На луче \( \small AH \) отложим отрезок \( \small HD \) так, чтобы \( \small AH=HD. \) Соединим точки \( \small C \) и \( \small D. \)

Треугольники \( \small AHB \) и \( \small DHC \) равны по двум сторонам и углу между ними (). Действительно: \( \small AH=HD, \) \( \small CH=HB, \) \( \small \angle 4=\angle 5 \) (углы 4 и 5 вертикальные). Тогда \( \small AB=CD, \) \( \small \angle 6=\angle 2. \) Отсюда \( \small \angle 6=\angle 1. \) Получили, что треугольник \( \small CAD \) равнобедренный (признак 2). Тогда \( \small AC=CD. \) Но \( \small AB=CD \) и, следовательно \( \small AB=AC. \) Получили, что треугольник \( \small ABC \) равнобедренный.

Свойства медианы треугольника

ОПРЕДЕЛЕНИЕ

Медиана треугольника — это сегмент, соединяющий вершину треугольника с серединой противоположной стороны.

Свойства медианов треугольника

Медиана делит треугольник на два треугольника равного размера (то есть на треугольники с одинаковой площадью).

Медианы треугольника пересекаются в одной точке, которая делит каждую из них в соотношении 2: 1, начиная с вершины. Эта точка называется центром тяжести треугольника.

• Весь треугольник делится на его медианы на шесть треугольников равного размера.
• В равнобедренном треугольнике медиана, опустившаяся до основания, является биссектрисой и высотой.
• В равностороннем треугольнике любая медиана — это высота и биссектриса.
• Примеры решения проблем
• ПРИМЕР 1

Задача

В равнобедренном треугольнике ( mathrm{ABC} ) со стороной ( A B=5 mathrm{см} ) медиана была ( B L=4 mathrm{см} ). Найдите область треугольника ( mathrm{ABC} ).

Решение.

1. Медиана делит треугольник на два треугольника равного размера, затем ( S_{Delta A B L}=S_{Delta B C L} ) , откуда
2. ( S_{Delta A B C}=2 S_{Delta A B L} )
3. Найдите область треугольника ( A B L ). Поскольку треугольник ( mathrm{ABC} ) является равнобедренным, медиана ( mathrm{BL} ) является высотой, то есть ( mathrm{ABL} ) треугольником — прямоугольной и ее площадью
4. ( S_{A B L}=frac{1}{2} A L cdot B L )
5. С помощью теоремы Пифагора мы находим ноги ( mathrm{AL} ):
6. ( A L=sqrt{A B^{2}-B L^{2}}=sqrt{25-16}=3 mathrm{cm} )
7. Замените полученные результаты в области формулы:
8. ( S_{A B L}=frac{1}{2} 3 cdot 4=6 mathrm{cm}^{2} )
9. Теперь мы находим область треугольника ( mathrm{ABC} ):
10. ( S_{A B C}=2 S_{A B L}=2 cdot 6=12 mathrm{cm}^{2} )

Ответ

• ( S_{A B C}=12 )
• ПРИМЕР 2

Задача

В треугольнике ( riangle B C ) со сторонами ( AB=4 mathrm{см} ), ( AC=6 mathrm{cm} ) и углом ( angle A=60^{circ} ) , мы выполнили медианны ( AK ) и ( BL ), которые пересекаются в точке ( O ). Найдите ( BO ).

Решение.

1. Так как ( BL ) — медиана треугольника,
2. ( A L=L C=frac{1}{2} A C=3 mathrm{cm} )
3. Рассмотрим треугольник ( ABL ). По теореме о косинуале находим
4. ( B L=sqrt{A B^{2}+A L^{2}-2 A B cdot A L cos angle A}=sqrt{16+9-2 cdot 4 cdot 3 cdot frac{1}{2}}=sqrt{13} mathrm{см} )

Медианы ( mathrm{AK} ) и ( BL ) пересекаются в точке, которая делит каждую из них в соотношении 2: 1, начиная с вершины, т.е.

$( B O=frac{2}{3} B L=frac{2 sqrt{13}}{3} mathrm{cm} )

Ответ

( B O=frac{2 sqrt{13}}{3} )

Нужны оригинальность, уникальность и персональный подход? Закажи свою оригинальную работу УЗНАТЬ СТОИМОСТЬ

Определение медианы

• Медианы треугольника пересекаются в одной точке и делятся этой точкой на две части в отношении 2:1, считая от вершины угла. Точка их пересечения называется центром тяжести треугольника (относительно редко в задачах для обозначения этой точки используется термин «центроид»), 
• Медиана разбивает треугольник на два равновеликих треугольника.
• Треугольник делится тремя медианами на шесть равновеликих треугольников.
• Большей стороне треугольника соответствует меньшая медиана.

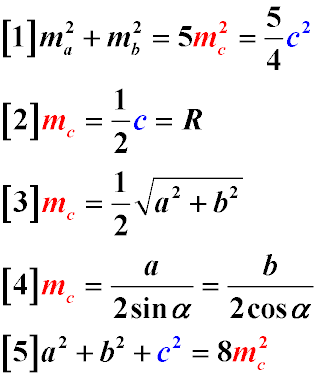
Задачи по геометрии, предлагаемые для решения, в основном, используют следующие свойства медианы прямоугольного треугольника.

• Сумма квадратов медиан, опущенных на катеты прямоугольного треугольника равна пяти квадратам медианы, опущенной на гипотенузу (Формула 1)
• Медиана, опущенная на гипотенузу прямоугольного треугольника равна половине гипотенузы (Формула 2)
• Медиана, опущенная на гипотенузу прямоугольного треугольника, равна радиусу окружности, описанной вокруг данного прямоугольного треугольника (Формула 2)
• Медиана, опущенная на гипотенузу, равна половине корня квадратного из суммы квадратов катетов (Формула 3)
• Медиана, опущенная на гипотенузу, равна частному от деления длины катета на два синуса противолежащего катету острого угла (Формула 4)
• Медиана, опущенная на гипотенузу, равна частному от деления длины катета на два косинуса прилежащего катету острого угла (Формула 4)
• Сумма квадратов сторон прямоугольного треугольника равна восьми квадратам медианы, опущенной на его гипотенузу (Формула 5)

Обозначения в формулах:

a, b — катеты прямоугольного треугольника

c — гипотенуза прямоугольного треугольника

Если обозначить треугольник, как ABC, то 

ВС = а

AC = b

AB = c

(то есть стороны a,b,c — являются противолежащими соответствующим углам)

m_a— медиана, проведенная к катету а 

m_b — медиана, проведенная к катету b

m_c — медиана прямоугольного треугольника, проведенная к гипотенузе с

α (альфа) — угол CAB, противолежащий стороне а

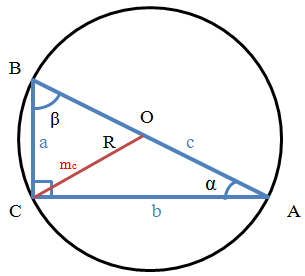
Точка пересечения биссектрис треугольника

Прежде чем мы приступим к изучению следующей точки, рассмотрим теорему о биссектрисе, проведённой из вершины неразвёрнутого угла, и докажем её.

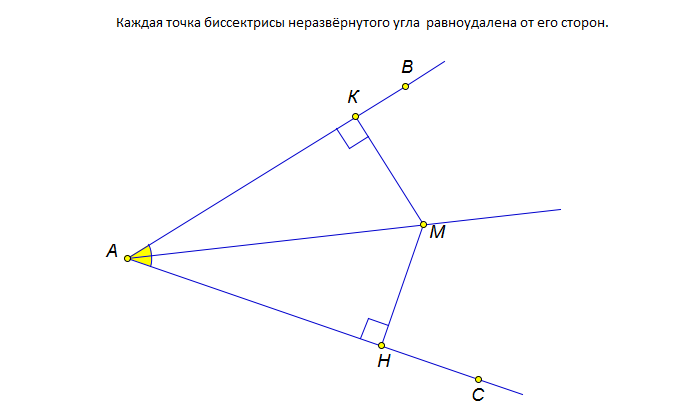
Рассмотрим пример. Дано:

• угол ВАС < 180 градусов;

• т. М лежит на прямой, исходящей из т. А;

• АМ — биссектриса угла ВАС (угол КАМ = углу МАН).

Доказать: точка М – равноудалённая от отрезков АВ и АС.

Доказательство.

Для начала достроим чертёж. Расстоянием от точки М до отрезка АС будет являться перпендикуляр МН. Аналогично и с остальной стороной (перпендикуляр МК). 

В треугольниках АКМ и АНМ:

• есть общая сторона – АМ;

• угол КАМ = МАН, так как АМ – биссектриса.

Сторона АМ является биссектрисой одновременно треугольников МКА и МНА, а при ней лежат равные углы. Значит треугольники равны (по гипотенузе и острому углу).

Так как треугольники равны, отрезки КМ и МН тоже равны, а значит т. М равноудалена от АВ и АС, что и требовалось доказать.

Переходим к построению замечательной точки.

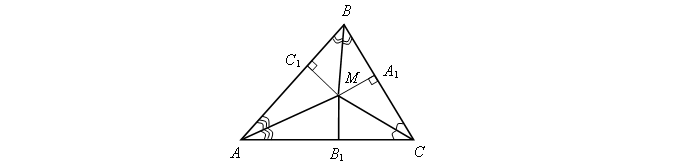
Отрезки С₁М, А₁М иВ₁М являются равными. Значит они однозначно могут быть радиусами вписанной в данный треугольник окружности. Это является свойством трёх пересекающихся биссектрис.

МЕДИАНА ТРЕУГОЛЬНИКА

Слово «медиана» переводится как «равноделящая сторону». Чтобы построить медиану, надо середину стороны треугольника соединить отрезком с противолежащей вершиной треугольника. Полученный отрезок и есть медиана треугольника.

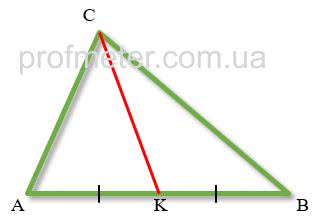
Медиана треугольника – отрезок, проведенный из вершины треугольника, соединяющий эту вершину с серединой противолежащей стороны треугольника.

На рисунке красным цветом обозначена медиана CK. При этом она делит сторону AB треугольника пополам, AK = KB.

Свойства медианы треугольника

Все медианы треугольника пересекаются в одной точке, расположенной в плоскости треугольника и являющейся его центром тяжести. 

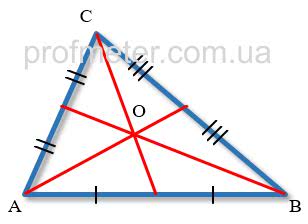
Для определения этой точки достаточно построить две медианы треугольника, и точка их пересечения будет принадлежать третьей медиане этого треугольника.

• Точкой пересечения медиан треугольника каждая медиана делится в отношении 2:1, считая от вершины треугольника. Т.е. длина отрезка медианы от вершины треугольника до точки пересечения медиан составляет 2/3 всей ее длины, а от точки пересечения медиан до стороны треугольника — 1/3 ее длины.

• Медиана разбивает треугольник на два равновеликих (по площади) треугольника.

• Треугольник делится тремя медианами на шесть равновеликих треугольников.

• Из отрезков, образующих медианы, можно составить треугольник, площадь которого будет равна 3/4 от всего треугольника. Длины медиан удовлетворяют неравенству треугольника.

• В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.

• Большей стороне треугольника соответствует меньшая медиана.

• У равнобедренного треугольника медиана, биссектриса и высота, проведенные к основанию треугольника, совпадают.

• У равностороннего треугольника все три «замечательные» линии (высота, биссектриса и медиана) совпадают и три «замечательных» точки (точки ортоцентра, центра тяжести и центра вписанной и описанной окружностей) находятся в одной точке пересечения «замечательных» линий, т.е. тоже совпадают.

Формулы медианы произвольного треугольника

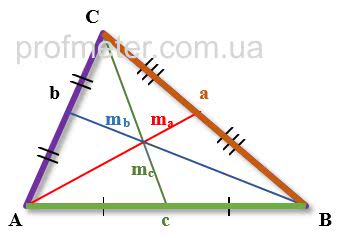
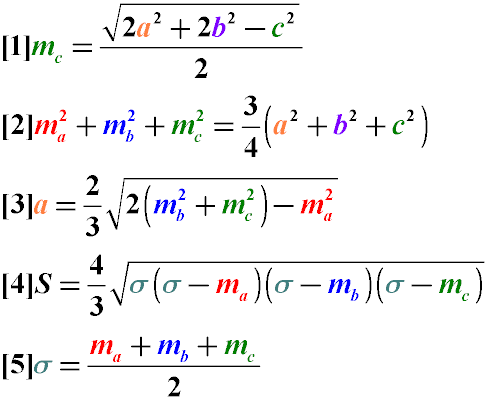
• Длина медианы, проведенной к стороне произвольного треугольника равна половине квадратного корня из удвоенной суммы квадратов двух других сторон из которой вычтен квадрат стороны, к которой проведена медиана (Формула 1)
• Сумма квадратов медиан треугольника равна 3/4 суммы квадратов его сторон (Формула 2)
• Длина стороны треугольника равна 2/3 квадратного корня из удвоенной суммы квадратов медиан, проведенных к двум другим его сторонам за вычетом квадрата медианы, проведенной к искомой стороне (Формула 3)
• Площадь треугольника можно найти через длины его медиан, используя значение полусуммы длин медиан (Формулы 4 и 5)

Содержание главы:

Как найти длину медианы треугольника

Нахождение площади через медианы

Угол между высотой и медианой треугольника

Медиана прямоугольного треугольника

Медіана прямокутного трикутника

Площадь треугольникаОписание курса Как найти длину медианы треугольника   

Расчет медианы в Excel

Медиану для числовых данных легко найти, используя функцию Excel, которая так и называется — МЕДИАНА. Другое дело интервальные данные. Соответствующей функции в Excel нет. Поэтому нужно задействовать приведенную выше формулу. Что поделаешь? Но это не очень трагично, так как расчет медианы по интервальным данным – редкий случай. Можно и на калькуляторе разок посчитать.

Напоследок предлагаю задачку. Имеется набор данных. 15, 5, 20, 5, 10. Каково среднее значение? Четыре варианта:

а) 11;

б) 5;

в) 10;

г) 5, 10, 11.

Мода, медиана и среднее значение выборки – это разный способ определить центральную тенденцию в выборке.

Ниже видеоролик о том, как рассчитать медиану в Excel.

https://youtube.com/watch?v=ZDHH8hogq0A

Равнобедренный треугольник (понятие):

Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой по длине.

Две равные стороны равнобедренного треугольника называются боковыми, а третья неравная им сторона – основанием.

Рис. 1. Равнобедренный треугольник

АВ = ВС – боковые стороны, АС – основание,

∠ АВС – вершинный угол, ∠ BАC и ∠ BСA – углы при основании

По определению, каждый правильный (равносторонний) треугольник также является равнобедренным, но не каждый равнобедренный треугольник – правильным (равносторонним).

Угол, образованный боковыми сторонами, называется вершинным углом, а углы, одной из сторон которых является основание, называются углами при основании.

Различают следующие виды равнобедренных треугольников:

– остроугольный – все углы острые;

– прямоугольный – угол при вершине прямой, а при основании углы острые;

– тупоугольный – угол при вершине тупой, а при основании углы острые;

– равносторонний (или правильный) – все стороны равны и все углы равны.

Формулы равнобедренного треугольника

Формулы сторон равнобедренного треугольника

b — основание равнобедренного треугольника

a — равные стороны равнобедренного треугольника

α — углы при основании

β — угол, образованный равными сторонами

Формулы длины стороны (основания b) равнобедренного треугольника

Формулы длины равных сторон равнобедренного треугольника (стороны a):

Формулы высоты, медианы, биссектрисы равнобедренного треугольника

b — основание равнобедренного треугольника

a — равные стороны равнобедренного треугольника

α — углы при основании

β — угол, образованный равными сторонами

L — высота, биссектриса и медиана

Формулы высоты, биссектрисы и медианы равнобедренного треугольника, через сторону и угол (L)

Формула высоты, биссектрисы и медианы равнобедренного треугольника, через стороны (L)

Теорема о медиане и площади треугольника

Почему? А давай вспомним самую простую форму площади треугольника. \( S=\frac{1}{2}a~\cdot h\).

И применим эту формулу аж два раза!

Посмотри, медиана \( \displaystyle BM\) разделила \( \displaystyle \triangle ABC\) на два треугольника: \( \displaystyle \triangle ABM\) и \( \displaystyle \triangle BMC\).

Но! Высота-то у них одна и та же – \( \displaystyle BH\)!

Только в \( \displaystyle \triangle ABM\) эта высота \( \displaystyle BH\) опускается на сторону \( \displaystyle AM\), а в \( \displaystyle \triangle BMC\) – на продолжение стороны \( \displaystyle CM\).

Удивительно, но вот бывает и так: треугольники разные, а высота – одна. И вот, теперь-то и применим два раза формулу

\( S=\frac{1}{2}a~\cdot h\).

1) B \( \displaystyle \triangle ABM\):

2) B \( \displaystyle \triangle BMC\):

Похожие записи:

Куриные отбивные в сырном кляре на сковороде Авокадо Сколько можно и как хранить бензин (в канистре, бутылке, баке авто) 7 самых красивых и неприхотливых комнатных папоротников Причины быстрой кристаллизации меда и ее связь с качеством продукта Можжевеловый веник для бани: польза и как пользоваться